Nombres complexes (trigonométrie et géométrie)

Sommaire

Introduction

Ce cours fait partie d'un ensemble de cours sur les nombres complexes :

une introduction : Nombres complexes (introduction) ,
deux cours qui recouvrent le programme de l'option "Mathématiques expertes" de classe terminale : celui-ci et un autre sur les équations en cours d'élaboration,
le cours Géométrie du plan complexe qui décrit les isométries et les similitudes du plan complexe avec exercices et figures.

Prérequis

Pour vous assurer de vos connaissances de base sur les nombres complexes, consultez le cours WIMS Nombres complexes (introduction) et testez-vous sur les exercices. Plus précisément, avant d'aborder la partie calcul algébrique, vérifiez que vous avez acquis les notions et les méthodes de la partie 2. Avant d'aborder la partie trigonométrie, vérifiez que vous avez acquis les notions et les méthodes de la partie 3. Pour la partie géométrique, travaillez les parties 1 et 4.

Ensuite vous pourrez poursuivre votre étude.

Pour compléter l'étude des équations à coefficients complexes, étudiez le cours Nombres complexes (équations) . En particulier, c'est dans ce cours que vous trouverez la résolution des équations en

z

\bar{z}

Trigonométrie

Formules de trigonométrie
Démonstrations de quelques formules de trigonométrie
Forme exponentielle, propriétés
Exercices
Formule de Moivre
Formules d'Euler et linéarisation
Somme d'exponentielles complexes
Écriture exponentielle et formules trigonométriques
Applications

Géométrie

Alignement et orthogonalité
Cercles
Détermination de lieux
Nombres complexes et suites (exercices).

Formule du binôme de Newton

La formule du binôme de Newton se démontre dans

ℂ

de la même façon que dans

ℝ

Formule du binôme de Newton.

Soient $n$ et $k$ deux entiers naturels, avec $k \leq n$ , on appelle coefficient binomial le nombre noté $(\binom{n}{k})$ défini par :

$(\binom{n}{k}) = \frac{n!}{(n - k)! k!}$

Si $a$ et $b$ sont deux nombres complexes, et $n$ un entier naturel, alors on a la formule suivante :

$(a + b)^{n} = \sum_{k = 0}^{k = n} (\binom{n}{k}) a^{n - k} b^{k} = \sum_{k = 0}^{k = n} (\binom{n}{k}) a^{k} b^{n - k}$

Nous verrons à la page Formules d'Euler et linéarisation une application de la formule du binôme de Newton à la trigonométrie.

Exercices. Application de la formule.

Calculer les expressions suivantes : $a = (1 + i)^{2}, b = (- 2 - 3 i)^{2}, c = (- 0, 5 + 2, 4 i)^{3}, d = (- 2 + 3 i)^{5}, e = (1 - 2 i)^{5}$

$a = 2 i, b = - 5 + 12 i, c = 8,515 - 12,024 i, d = - 122 - 597 i, e = 41 + 38 i$ .
Montrer que pour tout $n$ entier naturel : $(\binom{n}{0}) + (\binom{n}{1}) + (\binom{n}{2}) + (\binom{n}{3}) + \dots + (\binom{n}{n}) = 2^{n}$
Soit $n$ dans $ℕ^{*}$ , calculer les deux expressions : $A_{n} = \sum_{0 \leq 2 k \leq n} (\binom{n}{2 k})$ et $B_{n} = \sum_{0 \leq 2 k + 1 \leq n} (\binom{n}{2 k + 1})$

Il pourra être judicieux de calculer $A_{n} + B_{n}$ et $A_{n} - B_{n}$ .

$A_{n} = B_{n} = 2^{n - 1}$
Développement d'une puissance

Exercices. Coefficients binomiaux.

Quel est le coefficient du terme $a^{6} b^{7}$ dans le développement de $(2 a + i b)^{13}$

Le coefficient vaut : $- 109824 i$
Pour calculer des sommes.
1. Démontrer que, pour $1 \leq p \leq n$ , on a $p (\binom{n}{p}) = n (\binom{n - 1}{p - 1}) .$ En déduire $\sum_{p = 1}^{p = n} p (\binom{n}{p})$
2. Retrouver ce dernier résultat en dérivant $(1 + x)^{n}$

Équations linéaires

Il s'agit de résoudre, dans

ℂ

, le cas simple des équations du type

a z + b = 0

, où

a

b

sont des nombres complexes. La structure de

ℂ

permet de conduire les calculs comme dans

ℝ

. Pour l'étude générale, on procède par disjonction des cas et on note

𝒮

l’ensemble des solutions.

Règle.

Cas : $a = 0$ et $b = 0$ , l'équation admet tout nombre complexe pour solution : $𝒮 = ℂ$
Cas : $a = 0$ et $b \neq 0$ , l'équation n'a pas de solution : $𝒮 = \emptyset$
Cas : $a \neq 0$ , on ajoute $- b$ des deux cotés de l'égalité et on divise les deux membres par $a$ : $𝒮 = {- \frac{b}{a}}$

Exemple. Résoudre dans

ℂ

l'équation :

(1 + 2 i) z + 5 - 4 i = 0

En appliquant la méthode ci-dessus, on obtient :

z = - \frac{5 - 4 i}{1 + 2 i} = \frac{1}{5} (1 - 2 i) (- 5 + 4 i) = \frac{3}{5} + \frac{14}{5} i

Exemple aléatoire. Résoudre l'équation

() z =

. La solution est .

Exercices. Résoudre les équations suivantes.

$(2 + 2 i) z + (4 - 4 i) = 8 + 4 i$
$(5 - 2 i) z + (3 + 7 i) = \frac{23}{2} + 21 i$
$(1 + 5 i) z - 1 - 3 i = 27 - 19 i$

$𝒮 = {3 + i}$
$𝒮 = {\frac{1}{2} + 3 i}$
$𝒮 = {- 2 - 6 i}$

Les systèmes de deux équations linéaires à coefficients complexes, se résolvent, eux aussi, comme on le fait habituellement dans

ℝ

: par les méthodes d'addition, de substitution ou par la méthode du pivot.

Exercice. Résoudre dans

ℂ

le système :

{\begin{array}{rcrcrcr} (2 + 2 i) z + (2 - 3 i) z' = 23 + 4 i \\ (1 - i) z + (- 3 - 2 i) z' = 4 - 21 i \end{array}

La solution est : $z = 1 - i$ et $z' = 2 + 5 i$ .

Formules de trigonométrie

On se propose ici d'énoncer, puis de démontrer à la page suivante quelques-unes des formules de trigonométrie, on pourra les retrouver en utilisant les nombres complexes (voir Écriture exponentielle et formules trigonométriques ).

Pour $a$ , $b$ , $p$ et $q$ des nombres réels, et lorsque toutes les expressions sont bien définies :

Deux formules fondamentales.

$\cos^{2} a + \sin^{2} a = 1$ et $1 + \tan^{2} a = \frac{1}{\cos^{2} a}$

Formules de l'arc moitié.

$\cos 2 a = \cos^{2} a - \sin^{2} a = 2 \cos^{2} a - 1 = 1 - 2 \sin^{2} a$
$\sin 2 a = 2 \sin a \cos a$
$\tan 2 a = \frac{2 \tan a}{1 + \tan^{2} a}$
Si l'on pose $t = \tan \frac{a}{2}$ , alors on a : $\sin a = \frac{2 t}{1 + t^{2}} \cos a = \frac{1 - t^{2}}{1 + t^{2}} \tan a = \frac{2 t}{1 - t^{2}}$

Lignes trigonométriques de sommes ou différence.

$\sin (a - b) = \sin a \cos b - \sin b \cos a$
$\sin (a + b) = \sin a \cos b + \sin b \cos a$
$\cos (a + b) = \cos a \cos b - \sin a \sin b$
$\cos (a - b) = \cos a \cos b + \sin a \sin b$

Enfin, lorsque toutes les expressions sont bien définies :

$\tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b} \tan (a - b) = \frac{\tan a - \tan b}{1 + \tan a \tan b}$

Somme ou différence de lignes trigonométriques.

$\sin p + \sin q = 2 \sin \frac{p + q}{2} \cos \frac{p - q}{2}$
$\sin p - \sin q = 2 \sin \frac{p - q}{2} \cos \frac{p + q}{2}$
$\cos p + \cos q = 2 \cos \frac{p + q}{2} \cos \frac{p - q}{2}$
$\cos p - \cos q = - 2 \sin \frac{p - q}{2} \sin \frac{p + q}{2}$

Exercice. Calculs d'expressions du type cos(x+y)

Démonstrations de quelques formules de trigonométrie

Voici deux démonstrations du résultat : $\cos (a + b) = \cos a \cos b - \sin a \sin b$ pour $a$ et $b$ réels.

1. Démonstration avec le produit scalaire.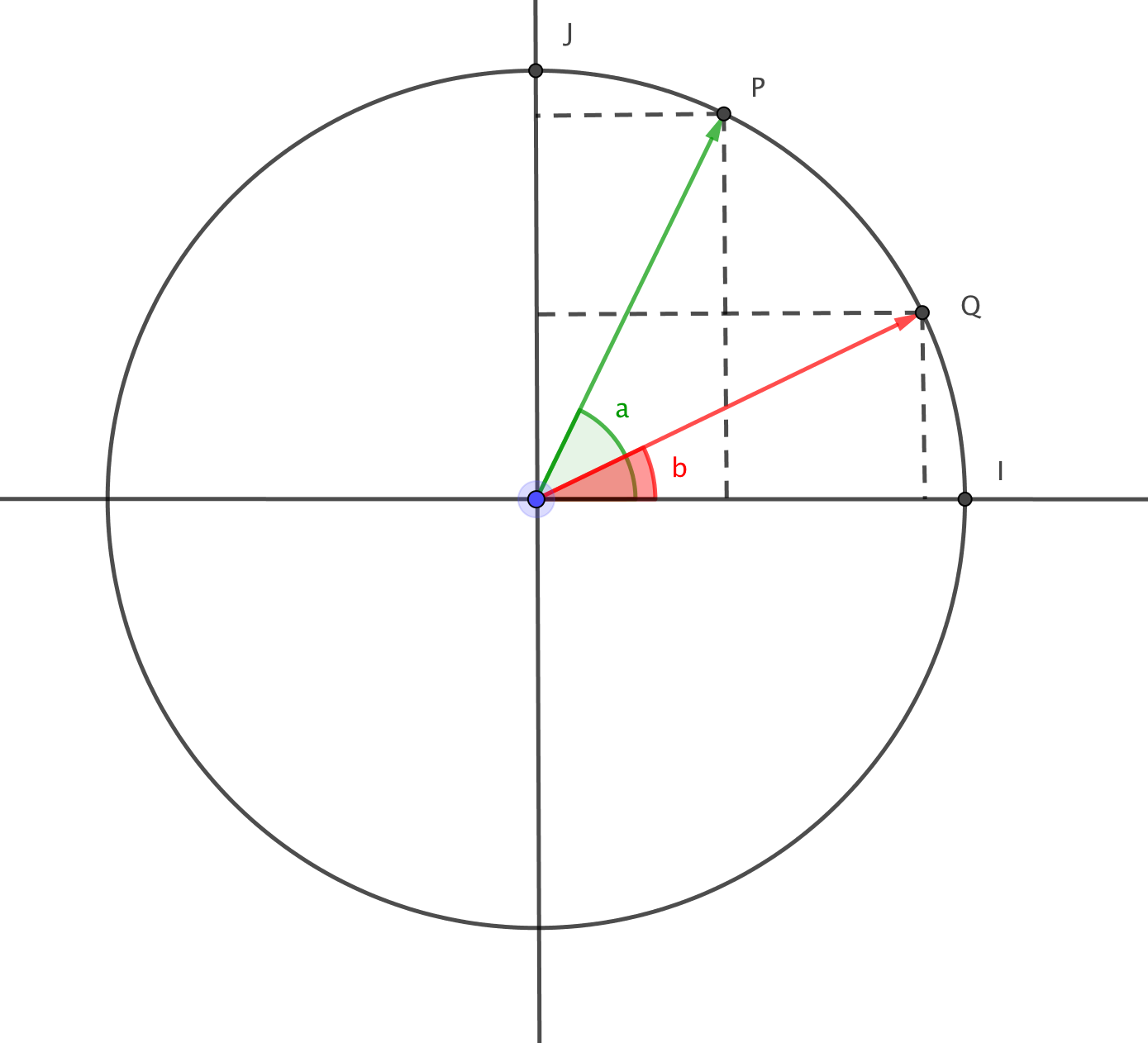

Dans le plan rapporté au repère orthonormé direct $(O, I, J)$ , on place sur le cercle unité deux points $P$ et $Q$ , avec $(I, \vec{OP}) = a [2 π]$ et $(I, \vec{OQ}) = b [2 π]$ . Le point $P$ a donc pour coordonnées $(\cos a, \sin a)$ et le point $Q$ a pour coordonnées $(\cos b, \sin b)$ . On écrit deux formes du produit scalaire $(\vec{OP} . \vec{OQ})$ :
$(\vec{OP} . \vec{OQ}) = \cos a \cos b + \sin a \sin b$ et $(\vec{OP} . \vec{OQ}) = ∥ \vec{OP} ∥ . ∥ \vec{OQ} ∥ \cos (\vec{OP}, \vec{OQ}) = \cos (b - a) = \cos (a - b)$

On a donc établi le résultat : $\cos (a - b) = \cos a \cos b + \sin a \sin b$ , et, en changeant $b$ en $- b$ , on obtient la formule : $\cos (a + b) = \cos a \cos b - \sin a \sin b$ .

2. Démonstration géométrique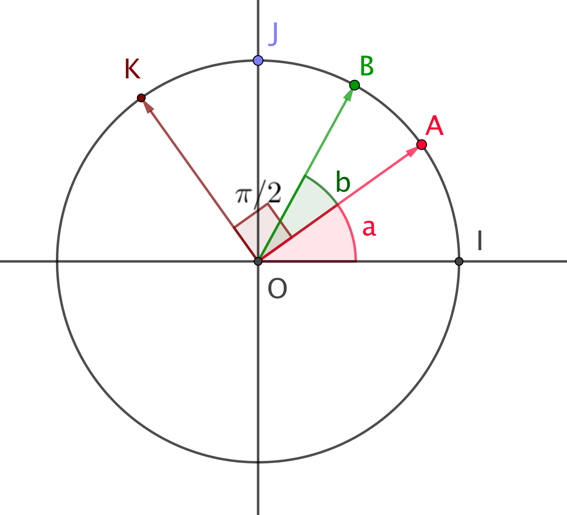

Dans le repère orthonormé direct $(O, I, J)$ , on considère sur le cercle unité trois points $A$ et $B$ et $K$ définis par $(\vec{OI}, \vec{OA}) = a [2 π]$ , $(\vec{OA}, \vec{OB}) = b [2 π]$ et $(\vec{OA}, \vec{OK}) = \frac{π}{2} [2 π]$
On en déduit : $\vec{OA} = \cos a \vec{OI} + \sin a \vec{OJ}$ et $\vec{OK} = \cos (a + \frac{π}{2}) \vec{OI} + \sin (a + \frac{π}{2}) \vec{OJ} = - \sin a \vec{OI} + \cos a \vec{OJ}$

Ecrivons le vecteur $\vec{OB}$ dans deux repères différents.
Dans le repère $(O, A, K)$ , on a $\vec{OB} = \cos b \vec{OA} + \sin b \vec{OK}$
Donc $\vec{OB} = \cos b [\cos a \vec{OI} + \sin a \vec{OJ}] + \sin b [- \sin a \vec{OI} + \cos a \vec{OJ}]$ $= (\cos a \cos b - \sin a \sin b) \vec{OI} + (\sin a \cos b + \sin b \cos a) \vec{OJ}$ (*)
Puis dans le repère $(O, I, J)$ , on a $\vec{OB} = \cos (a + b) \vec{OI} + \sin (a + b) \vec{OJ}$ (**)
Dans (*) et (**), on identifie les composantes en $\vec{OI}$ et on obtient $\cos (a + b) = \cos a \cos b - \sin a \sin b$ .
En considérant les composantes sur $\vec{OJ}$ on obtient : $\sin (a + b) = \sin a \cos b + \sin b \cos a$ .

On peut aussi retrouver ce résultat en utilisant des formes exponentielles complexes (voir Écriture exponentielle et formules trigonométriques ).

3. Démonstration du résultat :

\sin p + \sin q = 2 \sin \frac{(p + q)}{2} \cos \frac{(p - q)}{2}

, pour

p

q

réels.

On suppose connues les propriétés du sinus et du cosinus des sommes ou différences, dont l'une a été établie ci-dessus. De $\sin (a + b) = (\sin a \cos b + \sin b \cos a)$ et $\sin (a - b) = (\sin a \cos b - \sin b \cos a)$ , on déduit, par somme, $\sin (a + b) + \sin (a - b) = 2 \sin a \cos b$ .

Posons $a + b = p$ et $a - b = q$ , alors on a : $a = (\frac{p + q}{2})$ et $b = (\frac{p - q}{2})$ et la formule établie devient

$\sin p + \sin q = 2 \sin (\frac{p + q}{2}) \cos (\frac{p - q}{2})$

Les autres formules de la page Formules de trigonométrie se déduisent de celles-ci.

Forme exponentielle, propriétés

Les nombres complexes peuvent s'écrire sous différentes formes (voir cette page ), nous étudions ici plus particulièrement la forme exponentielle.

Notation.

On appelle forme exponentielle d'un nombre complexe non nul $z = r (\cos θ + i \sin θ)$ , de module $∣ z ∣ = r$ et d'argument $θ$ défini à $2 π$ près, l'écriture : $z = r e^{i θ}$ que l'on note également $z = r \exp (i θ)$ .

A ce niveau, cette écriture est une notation choisie pour sa pertinence dans les propriétés suivantes.

Propriétés. Soit

z, z_{1}, z_{2}

trois nombres complexes non nuls donnés sous forme exponentielle :

z = r e^{i θ}, z_{1} = r_{1} e^{i θ_{1}}, z_{2} = r_{2} e^{i θ_{2}}

avec

r

r_{1}

r_{2}

réels strictement positifs. Soit

n

est un entier naturel. Les formes exponentielles vérifient ces propriétés :

$z_{1} z_{2} = r_{1} e^{i θ_{1}} r_{2} e^{i θ_{2}} = r_{1} r_{2} e^{i (θ_{1} + θ_{2})}$
$z^{n} = (r e^{i θ})^{n} = r^{n} e^{i n θ}$
$\frac{1}{z} = \frac{1}{r e^{i θ}} = \frac{1}{r} e^{- i θ}$
$\frac{z_{1}}{z_{2}} = \frac{r_{1}}{r_{2}} e^{i (θ_{1} - θ_{2})}$

Ces propriétés sont démontrées dans la page Écriture exponentielle et formules trigonométriques .

Le cas particulier du nombre complexe de module 1 et d'argument

π

permet d'écrire :

e^{i π} = \cos π + i \sin π = - 1

Identité d'Euler. On appelle identité d'Euler la formule qui lie trois des constantes les plus importantes des mathématiques :

$e^{i π} = - 1$

Exercices

Exercice. On considère le nombre complexe

z = 4 + 4 i \sqrt{3}

. Donner ses formes trigonométrique et exponentielle.

$z = 8 e^{i \frac{π}{3}} = 8 [\cos \frac{π}{3} + i \sin \frac{π}{3}]$

Exercices : Autour de

\frac{π}{12}

Soit $z_{1} = \frac{\sqrt{6} - i \sqrt{2}}{2}$ et $z_{2} = 1 - i$ . Écrire sous forme exponentielle $Z = \frac{z_{1}}{z_{2}}$ .

On trouve $Z = e^{i \frac{π}{12}}$
Soit $z = \sqrt{2 + \sqrt{3}} + i \sqrt{2 - \sqrt{3}}$ . Calculer $z^{2}$ . En déduire l'écriture exponentielle de $z$ .

On fera attention au signe du sinus et du cosinus. On trouve : $z = 2 e^{i \frac{π}{12}}$
En remarquant que $\frac{π}{12} = \frac{π}{3} - \frac{π}{4}$ , montrer que : $\cos (\frac{π}{12}) = \frac{\sqrt{2} + \sqrt{6}}{4}$ et que $\sin (\frac{π}{12}) = \frac{\sqrt{6} - \sqrt{2}}{4}$
On considère le nombre complexe $z = (- 1 - i) (\frac{1}{2} - \frac{\sqrt{3}}{2} i)$ . On demande les valeurs de $\cos (\frac{11 π}{12})$ et de $\sin (\frac{11 π}{12})$ .

$\cos (\frac{11 π}{12}) = - (\frac{\sqrt{2} + \sqrt{6}}{4})$ et $\sin (\frac{11 π}{12}) = (\frac{\sqrt{6} - \sqrt{2}}{4})$

Exercice. Calculer

S = \sup_{∣ z ∣ = 1} ∣ z^{3} - z + 2 ∣^{2}

Il existe $x$ dans $ℝ$ tel que : $z = e^{i x}$ . Se rappeler que : $∣ z ∣^{2} = z \bar{z}$ . Exprimer $∣ z^{3} - z + 2 ∣^{2}$ comme polynôme en $\cos (x)$ . Chercher enfin les extremums de la fonction définie sur $[- 1, 1]$ , $t \to ϕ (t) = 8 - 16 t - 4 t^{2} + 16 t^{3}$

$𝒮 = 13$

Exercice.

Soit $z$ un nombre complexe. On note $z' = 1 + z + z^{2} + z^{3} + z^{4}$ . Montrer que si $z \neq 1$ , alors $z' = \frac{1 - z^{5}}{1 - z}$ .
Évaluer $z'$ si $z = e^{i \frac{2 π}{5}}$ . En déduire la valeur de $S = 1 + \cos \frac{2 π}{5} + \cos \frac{4 π}{5} + \cos \frac{6 π}{5} + \cos \frac{8 π}{5}$
Montrer que $\cos \frac{2 π}{5} + \cos \frac{8 π}{5} = 4 \cos^{2} \frac{π}{5} - 2$ , et que $\cos \frac{4 π}{5} + \cos \frac{6 π}{5} = - 2 \cos \frac{π}{5}$
En déduire que $\cos \frac{π}{5}$ est solution d'une équation du second degré, et donner sa valeur.

Formule de Moivre

Formule de Moivre. Soit

θ

un réel non nul et

n

un entier naturel. La traduction trigonométrique de la propriété :

(e^{i θ})^{n} = e^{i n θ}

est la formule de Moivre :

$\cos n θ + i \sin n θ = {[\cos θ + i \sin θ]}^{n}$

Application. À l'aide de la formule de Moivre et de la formule du binôme de Newton, on peut exprimer

\cos n θ

en fonction des puissances de

\cos θ

, c'est à dire sous forme d'un polynôme en

\cos θ

en utilisant la Formule du binôme de Newton .

Exemple. Pour

n = 2

, la formule de Moivre permet d'écrire

\cos 2 θ + i \sin 2 θ = (\cos θ + i \sin θ)^{2} = \cos^{2} θ + 2 i \sin θ \cos θ - \sin^{2} θ

On en déduit, par exemple, en égalant les parties réelles et imaginaires :

\cos 2 θ = \cos^{2} θ - \sin^{2} θ = 2 \cos^{2} θ - 1 = 1 - 2 \sin^{2} θ

\sin 2 θ = 2 \sin θ \cos θ

Exemple aléatoire.

En utilisant l'expression de la puissance $n$ -ième d'une somme à l'aide des coefficients binomiaux, on obtient

$\cos (4 * x) + i \sin (4 * x) = .$

On sépare ensuite les parties réelles et imaginaires.

Exercice.
Soit

θ

un réel non nul, montrer que :

$\cos 3 θ = 4 \cos^{3} (θ) - 3 \cos θ$
$\sin 3 θ = 3 \sin θ - 4 \sin^{3} θ$
$\cos 5 θ = \cos^{5} θ - 10 \cos^{3} θ \sin^{2} θ + \cos θ \sin^{4} θ$
$\sin 5 θ = \sin^{5} θ - 10 \sin^{3} θ \cos^{2} θ + \sin θ \cos^{4} θ$

Exercice.
Calculer

S = 1 + (\binom{n}{1}) \cos x + (\binom{n}{2}) \cos 2 x + \dots + (\binom{n}{n}) \cos n x

On pourra poser $S' = (\binom{n}{1}) \sin x + (\binom{n}{2}) \sin 2 x + \dots + (\binom{n}{n}) \sin n x$ , puis calculer $S + i S'$ .

$S = 2^{n} \cos^{n} (\frac{x}{2}) \cos n \frac{x}{2}$ .

Exercice.
Calculer, à l'aide de la formule de Moivre pour

n = 5

\cos 5 a

en fonction de

\cos a

. En déduire la valeur de

\cos \frac{π}{10}

$\cos 5 a = 16 \cos^{5} a - 20 \cos^{3} a + 5 \cos a$
$\cos \frac{π}{10} = \sqrt{\frac{5 + \sqrt{5}}{8}}$

Formules d'Euler et linéarisation

Les deux écritures $e^{i x} = \cos x + i \sin x$ et $e^{- i x} = \cos x - i \sin x$ , permettent d'exprimer les sinus et cosinus en fonction d'exponentielles complexes. On arrive facilement aux formules d'Euler :

Formules d'Euler.

Pour tout $x$ réel, on a : $\cos x = \frac{e^{i x} + e^{- i x}}{2}$ et $\sin x = \frac{e^{i x} - e^{- i x}}{2 i}$

Application. Linéarisation des polynômes trigonométriques

Intégrer des polynômes trigonométriques, c'est-à-dire des polynômes en sinus et cosinus, se révèle parfois peu évident. La technique dite de linéarisation des polynômes trigonométriques est dans certains cas d'une aide précieuse.Elle consiste à transformer les puissances $\cos (x)^{p}$ , $\sin (x)^{q}$ en sommes et multiples d'expressions du type $\cos (rx)$ ou $\sin (sx)$ . On utilise pour cela les formules d'Euler, successivement dans les deux sens. (Voir Application à l'intégration )

Exemple : Linéariser

\sin^{3} x

\sin^{3} x = {(\frac{e^{i x} - e^{- i x}}{2 i})}^{3}

= (\frac{1}{8 i^{3}}) (e^{3 i x} - 3 e^{2 i x} e^{- i x} + 3 e^{i x} e^{- 2 i x} - e^{- 3 i x})

= (- \frac{1}{8}) (\frac{e^{3 i x} - e^{- 3 i x}}{i} - 3 \frac{e^{i x} - e^{- i x}}{i})

= \frac{3 \sin x - \sin 3 x}{4}

Exercices. Linéariser

\sin^{2} x \cos^{3} x

, puis

\sin^{3} x \cos^{3} x

, puis

\cos^{4} x

, puis

\sin^{3} x \cos^{2} x

\sin^{2} x \cos^{3} x = - \frac{1}{16} \cos 5 x - \frac{1}{16} \cos 3 x + \frac{1}{8} \cos x

\sin^{3} x \cos^{3} x = - \frac{1}{32} \sin 6 x + \frac{3}{32} \sin 2 x

\cos^{4} x = \frac{1}{8} \cos 4 x + \frac{1}{2} \cos 2 x + \frac{3}{8}

\sin^{3} x \cos^{2} x = - \frac{1}{16} \sin 5 x + \frac{1}{16} \sin 3 x + \frac{1}{8} \sin x

Exercice. Donner la forme trigonométrique de

A_{n} = (1 + i)^{n} + (1 - i)^{n}

Le nombre $A_{n}$ est réel, comme somme d'un complexe et de son conjugué ; son signe (car il il n'est pas toujours positif) va déterminer l'argument... Il va falloir regarder le signe de $\cos (n \frac{π}{4})$ ...

A_{n} = (\sqrt{2})^{n + 2} \cos (n \frac{π}{4})

$\cos (n \frac{π}{4}) > 0 \Leftrightarrow n = 8 k + p, \forall k \in ℤ et p \in {0, 1, 7}$ . On a donc : $A_{n} = (\sqrt{2})^{n + 2} \cos (n \frac{π}{4}) [\cos 0 + i \sin 0]$
$\cos (n \frac{π}{4}) < 0 \Leftrightarrow n = 8 k + p, \forall k \in ℤ et p \in {3, 4, 5}$ . On a donc : $A_{n} = - (\sqrt{2})^{n + 2} \cos (n \frac{π}{4}) [\cos π + i \sin π]$
$\cos (n \frac{π}{4}) = 0 \Leftrightarrow n = 8 k + p, \forall k \in ℤ et p \in {2, 6}$ . On a donc : $A_{n} = 0$

Exercice. Pour calculer des sommes avec des nombres complexes. (Plus difficile)
On pose

j = \frac{- 1 + i \sqrt{3}}{2}

Montrer que la suite $(j^{n})_{n \in ℕ}$ est périodique de période 3 (on écrira les dix premiers termes de cette suite).
Pour $n \in ℕ$ , calculer les trois sommes $A = (\binom{n}{0}) + (\binom{n}{3}) + (\binom{n}{6}) + \dots$ , $B = (\binom{n}{1}) + (\binom{n}{4}) + (\binom{n}{7}) + \dots$ , $C = (\binom{n}{2}) + (\binom{n}{5}) + (\binom{n}{8}) + \dots$ .
Ces trois sommes sont finies, le $k$ des $(\binom{n}{k})$ étant toujours inférieur ou égal à $n$ .

On intéressera aux trois sommes $A + B + C, A + j B + j^{2} C, A + j^{2} B + j C,$ en faisant apparaître des développements de binôme de Newton.

$A + B + C = 2^{n}; A + j B + j^{2} C = (1 + j)^{n} = e^{i n \frac{π}{3}}; A + j^{2} B + j C = (1 + j^{2})^{n} = e^{- i n \frac{π}{3}}$
En se souvenant que $1 + j + j^{2} = 0$ , on combinera, en les multipliant par des coefficients judicieux et en les additionnant, les trois égalités ci-dessus pour faire disparaitre à chaque fois deux des trois termes $A, B$ ou $C$
$A = \frac{1}{3} [2^{n} + 2 \cos n \frac{π}{3}], B = \frac{1}{3} [2^{n} + 2 \cos (n - 2) \frac{π}{3}], C = \frac{1}{3} [2^{n} + 2 \cos (n + 2) \frac{π}{3}]$
N.B. En conduisant les calculs différemment (sans faire aucune erreur de calcul) on peut arriver à des résultats un peu différents de ceux qui sont indiqués ci-dessus. En fait, ce sera bien le même résultat, sous une autre forme, et il peut être instructif de retrouver ceux qui sont donnés ici.

Somme d'exponentielles complexes

Pour simplifier une somme faisant intervenir une ou des exponentielles complexes, la méthode de factorisation par l'argument moitié peut être utile. Voyons cela sur un exemple. On veut mettre sous forme exponentielle $A = 1 + e^{i α}$ où $α$ est un réel quelconque. L'idée efficace est de factoriser $A$ par $e^{i \frac{α}{2}}$ , ce qui donne :

$A = 1 + e^{i α} = e^{i \frac{α}{2}} (e^{- i \frac{α}{2}} + e^{i \frac{α}{2}}) = e^{i \frac{α}{2}} (2 \cos \frac{α}{2})$ .

On s'est approché du but : on a fait apparaitre $2 \cos \frac{α}{2}$ qui est réel, et l’exponentielle complexe $e^{i \frac{α}{2}}$ . Mais $2 \cos \frac{α}{2}$ n'est pas nécessairement le module de $A$ , car il n'est pas toujours positif. Il faut donc un peu poursuivre le travail et préciser son signe. Mais la méthode utilisée a permis de progresser ! Il reste à s'intéresser au signe de $2 \cos \frac{α}{2}$ . Ceci est développé

Cas $\cos \frac{a}{2} \geq 0$
$\cos \frac{a}{2} \geq 0 ⟺ - \frac{π}{2} + 2 k π \leq \frac{a}{2} \leq \frac{π}{2} + 2 k π ⟺ - π + 4 k π \leq - 2 \leq π + 4 k π (k \in ℤ)$
Si $a$ vérifie $- π + 4 k π \leq - 2 \leq π + 4 k π (k \in ℤ)$ , alors $A = 2 \cos \frac{a}{2} e^{i \frac{α}{2}}$
Cas $\cos \frac{a}{2} \leq 0$
$\cos \frac{a}{2} \leq 0 ⟺ \frac{π}{2} + 2 k π \leq \frac{a}{2} \leq 3 \frac{π}{2} + 2 k π ⟺ π + 4 k π \leq - 2 \leq 3 π + 4 k π (k \in ℤ)$
Quand le nombre $\cos \frac{a}{2}$ est négatif, sa forme exponentielle est $\cos \frac{a}{2} = (- \cos \frac{a}{2}) e^{i π}$ ; alors on a $A = (- 2 \cos \frac{a}{2}) e^{i π} e^{i \frac{α}{2}} = (- 2 \cos \frac{a}{2}) e^{i (π + \frac{α}{2})}$ .
Si $a$ vérifie $π + 4 k π \leq - 2 \leq 3 π + 4 k π (k \in ℤ)$ , alors $A = (- 2 \cos \frac{a}{2}) e^{i (π + \frac{α}{2})}$ .

Application à : $\sin p - \sin q = 2 \sin (\frac{p - q}{2}) \cos (\frac{p + q}{2})$

Les formules d'Euler permettent d'écrire :

(\sin p - \sin q) = \frac{1}{2 i} (e^{i p} - e^{- i p} - e^{i q} + e^{- i q})

.
La bonne idée est ici de mettre en facteur

e^{i \frac{p + q}{2}}

dans la partie

e^{i p} - e^{i q}

e^{i p} - e^{iq} = e^{i \frac{p + q}{2}} (e^{i \frac{p - q}{2}} - e^{i \frac{- p + q}{2}}) = e^{i \frac{p + q}{2}} 2 i \sin (\frac{p - q}{2})

puis on met en facteur

e^{i \frac{- p - q}{2}}

dans la partie

e^{- i p} - e^{- i q}

e^{- i p} - e^{- i q} = e^{i \frac{- p - q}{2}} (e^{i \frac{- p + q}{2}} - e^{i \frac{p - q}{2}}) = e^{i \frac{- p - q}{2}} 2 i \sin (\frac{- p + q}{2})

En regroupant ces deux résultats, on obtient :

\sin p - \sin q = \frac{1}{2 i} [(e^{i \frac{p + q}{2}} 2 i \sin (\frac{p - q}{2}) - e^{i \frac{- p - q}{2}} 2 i \sin (\frac{- p + q}{2})] = \frac{1}{2} [2 \sin (\frac{p - q}{2}) (e^{i \frac{p + q}{2}} + e^{i \frac{- p - q}{2}})] = 2 \sin (\frac{p - q}{2}) \cos (\frac{p + q}{2})

Exercices.

Mettre sous forme trigonométrique le nombre complexe $z = e^{i x} + e^{i y}$ , sachant que $- \frac{π}{2} < \frac{x - y}{2} < \frac{π}{2}$

Comme, ici, $\cos \frac{x - y}{2}$ est positif, $z$ a pour forme exponentielle $2 \cos \frac{x - y}{2} e^{i \frac{x + y}{2}}$ et pour forme trigonométrique $2 \cos \frac{x - y}{2} [\cos \frac{x + y}{2} + i \sin \frac{x + y}{2}]$
Soit $a \in ℝ - π ℤ$ . Quel est le module et l'argument de $z = \frac{1 + \cos a + i \sin a}{1 - \cos a - i \sin a}$ ?

$z = \frac{1 + e^{i a}}{1 - e^{i a}} = \frac{e^{i \frac{a}{2}} [e^{- i \frac{a}{2}} + e^{i \frac{a}{2}}]}{e^{i \frac{a}{2}} [e^{- i \frac{a}{2}} - e^{i \frac{a}{2}}]} = \frac{2 \cos \frac{a}{2}}{- 2 i \sin \frac{a}{2}} = \frac{i}{\tan \frac{a}{2}}$
On en déduit : $∣ z ∣ = \frac{1}{∣ \tan \frac{a}{2} ∣} = ∣ cotan \frac{a}{2} ∣$ et $\arg z = \arg (i) - \arg (\tan \frac{a}{2}) = \frac{π}{2} - \arg (\tan \frac{a}{2}) [2 π]$ .
Pour calculer $\arg (\tan \frac{a}{2})$ , on étudie le signe du réel $\tan \frac{a}{2}$ .
• Pour $\tan \frac{a}{2} > 0$ , $\arg (\tan \frac{a}{2}) = 0$ et $\arg z = \frac{π}{2} [2 π]$
• Pour $\tan \frac{a}{2} < 0$ , $\arg (\tan \frac{a}{2}) = π$ et $\arg z = - \frac{π}{2} [2 π]$
Soit $n \in ℕ$ et $x$ un réel quelconque. Calculer $S_{n} = \sum_{k = 0}^{n} \cos (kx)$ .

Pensez que $\cos (k x) = ℛ e (e^{i k x})$ et calculez $\sum_{k = 0}^{n} e^{i kx}$ dont il suffira de conserver la partie réelle.
Comme plus haut, dans l'expression $1 - e^{i x}$ , on peut factoriser par $e^{i \frac{x}{2}}$ , ce qui donne: $1 - e^{i x} = e^{i \frac{x}{2}} (e^{- i \frac{x}{2}} - e^{i \frac{x}{2}})$
Enfin ne pas oublier le cas où $x = 0$

Pour $x \neq 0 S_{n} = \cos (n \frac{x}{2}) \frac{\sin (n + 1) \frac{x}{2}}{\sin \frac{x}{2}}$
Pour $x = 0 S_{n} = n + 1$ .

Écriture exponentielle et formules trigonométriques

Nous démontrons ici la première propriété de la forme exponentielle (voir cette page ) en nous appuyant sur les Formules de trigonométrie mais surtout nous montrons comment les propriétés de la forme exponentielle et les formules d'Euler permettent de retrouver les formules de trignométrie

Démonstration de : $z_{1} z_{2} = r_{1} e^{i θ_{1}} r_{2} e^{i θ_{2}} = r_{1} r_{2} e^{i (θ_{1} + θ_{2})}$

Soit

z_{1} = r_{1} e^{i θ_{1}} = r_{1} [\cos θ_{1} + i \sin θ_{1}]

z_{2} = r_{2} e^{i θ_{2}} = r_{2} [\cos θ_{2} + i \sin θ_{2}]

z_{1} z_{2} = r_{1} [\cos θ_{1} + i \sin θ_{1}] r_{2} [\cos θ_{2} + i \sin θ_{2}]

z_{1} z_{2} = r_{1} r_{2} [(\cos θ_{1} \cos θ_{2} - \sin θ_{1} \sin θ_{2}) + i (\sin θ_{1} \cos θ_{2} + \sin θ_{2} \cos θ_{1})]

z_{1} z_{2} = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + i \sin (θ_{1} + θ_{2})]

z_{1} z_{2} = r_{1} r_{2} e^{i (θ_{1} + θ_{2})}

La notation exponentielle et les formules d'Euler aident à retrouver facilement les formules trigonométriques.

Exemples.

$\cos (a + b) = \cos a \cos b - \sin a \sin b$ .
Soit $a$ et $b$ deux nombres réels. On écrit les formes trigonométriques du résultat qui vient d'être vu : $e^{i (a + b)} = e^{i a} e^{i b}$
$\cos (a + b) + i \sin (a + b) = (\cos a + i \sin a) (\cos b + i \sin b) = (\cos a \cos b - \sin a \sin b) + i (\sin a \cos b + \sin b \cos a)$
On obtient $\cos (a + b)$ (et $\sin (a + b)$ ), en égalant les parties réelles et imaginaires.
Toutes les autres formules se retrouvent de même.
$\cos a \cos b = \frac{1}{2} (\cos (a + b) + \cos (a - b))$ .
$\cos a \cos b = \frac{1}{4} (e^{i a} + e^{- i a}) (e^{i b} + e^{- i b}) = \frac{1}{4} (e^{i (a + b)} + e^{i (a - b)} + e^{- i (a - b)} + e^{- i (a + b)})$ . Le résultat en découle.

Equations trigonométriques

Rappelons les trois résultats élémentaires, mais fondamentaux, sur les équations trigonométriques.

Propriétés
Soit

a, b, c

trois réels,

- 1 \leq a \leq 1

- 1 \leq b \leq 1

c

réel quelconque.

Équation : $\cos x_{1} = a$ . On cherche s'il existe un réel $α$ tel que $\cos α = a$ .
L'équation admet alors les solutions : $x_{1} = \pm α + 2 k π$ ( $k \in ℤ$ )
Équation : $\sin x_{2} = b$ . On cherche s'il existe un réel $β$ tel que $\sin β = a$ .
L'équation admet alors les solutions : $x_{2} = β + 2 k π$ , et $x'_{2} = π - β + 2 k π$ ( $k \in ℤ$ )
Équation : $\tan x_{3} = c$ . On cherche s'il existe un réel $γ$ tel que $\tan γ = c$ .
L'équation admet alors les solutions : $x_{3} = γ + k π$ ( $k \in ℤ$ )

Pour trouver les valeurs $α, β, γ$ , on peut, s'il ne s'agit pas d'angles remarquables connus, utiliser une calculatrice et les touches des fonctions trigonométriques directes et inverses. Cela dépend des calculatrices : soit les touches arccos, arcsin, arctan ou, sur d'autres, avec deux touches inv/cos, inv/sin, inv/tan ou 2nd/cos , 2nd/sin, 2nd/tan

Exemple : Pour

x = - 0, 7

, on obtient (en radians) :

\arccos x = 2,346 19

\arcsin x = - 0,775 397

\arctan x = - 0,610 726

Exercices.

Résoudre dans $ℝ$ :
- $\cos (x + \frac{π}{4}) + \sin (2 x - \frac{π}{3}) = 0$
  $x = \frac{π}{12} + 2 k π$ avec $k \in ℤ$ ou $x = - \frac{5 π}{36} + 2 k \frac{π}{3}$ avec $k \in ℤ$
- $\cos 2 x - 11 \cos x + 6 > 0$
  On rappelle que $\cos (2 x) = 2 \cos (x)^{2} - 1$ . Poser ensuite $X = \cos (x)$ , puis résoudre l'équation $X^{2} - 11 X + 5 > 0$ .
  La solution est : $\frac{π}{3} + 2 k π < x < \frac{5 π}{3} + 2 k π (k \in ℤ)$
Nombre de solutions d'une équation trigonométrique
Solutions d'une équation trigonométrique

Equations trigonométriques (suite)

Étude de l'équation :

a \cos x + b \sin x = c

avec

a, b, c

réels, et

(a, b) \neq (0, 0)

Méthode générale. On divise les deux membres de l'équation à résoudre par $\sqrt{a^{2} + b^{2}}$ , ce qui conduit à l'équation :

$\frac{a}{\sqrt{a^{2} + b^{2}}} \cos x$ + $\frac{b}{\sqrt{a^{2} + b^{2}}} \sin x = \frac{c}{\sqrt{a^{2} + b^{2}}}$ .

Posons $α = \frac{a}{\sqrt{a^{2} + b^{2}}}$ et $β = \frac{b}{\sqrt{a^{2} + b^{2}}}$ . On remarque que $α^{2} + β^{2} = 1$ . Égalité à rapprocher de : $\cos^{2} θ + \sin^{2} θ = 1$ . Par identification, mais c'est un théorème qui le justifie, il existe $θ$ réel, défini à $2 π$ près, vérifiant :

$\cos θ = α = \frac{a}{\sqrt{a^{2} + b^{2}}}$ et $\sin θ = β = \frac{b}{\sqrt{a^{2} + b^{2}}}$

L'équation s'écrit maintenant :

$\cos θ \cos x + \sin θ sinx = \frac{c}{\sqrt{a^{2} + b^{2}}}$ ou encore : $\cos (x - θ) = \frac{c}{\sqrt{a^{2} + b^{2}}}$ .

Ceci ouvre à une discussion suivant les valeurs de

C = \frac{c}{\sqrt{a^{2} + b^{2}}}

Dans le cas $C \in] - ∞, - 1 [\cup] 1, + ∞ [$ , l'équation n'admet pas de solution.
Dans le cas $- 1 \leq C \leq 1$ , il existe $γ \in [0, 2 π [$ vérifiant $\cos γ = C$ .
L'équation s'écrit maintenant : $\cos (x - θ) = \cos (γ)$
L'ensemble des solutions est donc ${γ + θ + 2 k π (k \in ℤ)} \cup$ ${- γ + θ + 2 k' π (k' \in ℤ)}$ .

Exercices. Résoudre les équations :

$\cos 2 x + \sqrt{3} \sin 2 x = \sqrt{2}$

$𝒮 = {\frac{7 π}{24} + k π (k \in ℤ)} \cup$ ${\frac{π}{24} + k' π (k' \in ℤ)}$
$\cos 3 x + \sin 3 x = 1$

$𝒮 = {\frac{π}{6} + \frac{2 k π}{3} (k \in ℤ)} \cup$ ${\frac{2 k' π}{3} (k' \in ℤ)}$
$\cos x + \sqrt{3} \sin x = - 1$

$𝒮 = {π + 2 k π (k \in ℤ)} \cup$ ${- \frac{π}{3} + 2 k' π (k' \in ℤ)}$

Application à l'intégration

Si on veut intégrer des expressions du type $\begin{array}{c} \int \end{array} P [\sin^{p} x, \cos^{q} x] d x$ avec $(p, q) \in ℕ^{2}$ et $P$ un polynôme, en particulier lorsque $p$ et $q$ sont pairs, on utilise la linéarisation (voir ici ) pour les termes en $\sin^{p} x$ et $\cos^{q} x$ . Si $p$ ou $q$ est impair, on peut aussi reconnaître une dérivée et faire un changement de variable (voir un cours sur l'intégration).

Exemple. Calcul de

I = \begin{array}{c} \int \end{array} \sin^{4} x \cos^{2} x dx

\sin^{4} x \cos^{2} x = (\frac{1}{2 i})^{4} (e^{i x} - e^{- i x})^{2} (\frac{1}{2})^{2} (e^{i x} + e^{- i x})^{2} = \dots = (\frac{1}{32}) (e^{6 i x} + e^{- 6 i x} - 2 (e^{4 i x} + e^{- 4 i x}) - (e^{2 i x} + e^{- 2 i x}) + 4

= (\frac{1}{32}) (2 \cos 6 x - 4 \cos 4 x - 2 \cos 2 x + 4)

. L'intégration se fait sans difficulté maintenant puisqu'une primitive de

\cos (n x)

est

\frac{\sin n x}{n}

.
On trouve

I = \frac{1}{192} \sin 6 x - \frac{1}{64} \sin 4 x - \frac{1}{64} \sin 2 x + \frac{1}{16} x + C

, où

C

est une constante quelconque.

Exercice . Calculer

I = {\begin{array}{c} \int \end{array}}_{0}^{\frac{π}{2}} \sin^{2} x \cos^{3} x dx

, en linéarisant l'expression à intégrer.

Une primitive est : $\frac{1}{8} \sin x - \frac{1}{48} \sin 3 x - \frac{1}{80} \sin 5 x$ . Et $I$ vaut $\frac{2}{15}$

Exercice . Calculer

I = {\begin{array}{c} \int \end{array}}_{0}^{\frac{π}{2}} \sin^{3} x \cos^{3} x dx

, en linéarisant l'expresssion à intégrer.

Une primitive est : $- \frac{3}{64} \cos 2 x + \frac{1}{192} \cos 6 x$ . Et $I$ vaut $\frac{1}{12}$

Puissance entière d'un nombre complexe.

Pour le calcul de puissance entière d'un nombre complexe, sa forme trigonométrique est souvent plus utile que la forme algébrique.

Soit $z \in ℂ$ , mis sous forme trigonométrique : $z = ρ (\cos θ + i \sin θ)$ ,( $ρ > 0$ et $θ$ réels).
On utilisera le résultat $z^{n} = ρ^{n} (\cos n θ + i \sin n θ)$ .

Exercices.

Soit $Z = {(\frac{1 + i \sqrt{3}}{1 + i})}^{125}$ .
1. Donner sa forme exponentielle.
2. Calculer sa partie réelle et sa partie imaginaire. On pourra s'aider de cette page
1. $(\frac{1 + i \sqrt{3}}{1 + i}) = \sqrt{2} e^{i \frac{π}{12}}$ et ${(\frac{1 + i \sqrt{3}}{1 + i})}^{125} = {\sqrt{2}}^{125} e^{i \frac{125 π}{12}}$ .
  Il faut chercher combien de fois il y a de $2 π = \frac{24 π}{12}$ dans $\frac{125 π}{12}$ . On fait donc la division euclidienne de $125$ par 24. $125 = 5 \times 24 + 5$ , donc $\frac{125 π}{12} = 5 \frac{24 π}{12} + 5 \frac{π}{12} = 5 \frac{π}{12} [2 π]$
  Et $Z = {\sqrt{2}}^{125} e^{i \frac{5 π}{12}}$ .
2. ${\sqrt{2}}^{125} e^{i \frac{5 π}{12}} = {\sqrt{2}}^{125} [\cos \frac{5 π}{12} + i \sin \frac{5 π}{12}]$
  On remarque que $\frac{5 π}{12} = \frac{π}{2} - \frac{π}{12}$ .
  Donc $\cos \frac{5 π}{12} = \sin \frac{π}{12} = \frac{\sqrt{6} - \sqrt{2}}{4}$ et $\sin \frac{5 π}{12} = \cos \frac{π}{12} = \frac{\sqrt{2} + \sqrt{6}}{4}$
  $Z = {\sqrt{2}}^{125} e^{i \frac{5 π}{12}} = 2^{62} \sqrt{2} [\frac{\sqrt{2} (\sqrt{3} - 1)}{4} + i \frac{\sqrt{2} (\sqrt{3} + 1)}{4}]$ d'où le résultat :
  $ℛ e Z = 2^{61} (\sqrt{3} - 1)$ et $ℐ m Z = 2^{61} (\sqrt{3} + 1)$
Calculer $Z = {(\frac{\sqrt{2} + i \sqrt{2}}{\sqrt{3} - i})}^{2020}$
$Z = e^{i \frac{5 π}{3}} = \frac{1}{2} - i \frac{\sqrt{3}}{2}$
Calculer $Z = {(\frac{1 + i \sqrt{3}}{1 - i})}^{20}$
$Z = 2^{10} e^{- i \frac{π}{3}}$

Alignement et orthogonalité

On considère 4 points $A, B, C, D$ d'affixes respectives $a, b, c, d$ .

Orthogonalité.
Les propositions suivantes sont équivalentes et signifient l'orthogonalité des vecteurs

\vec{AB}

\vec{CD}

$(\vec{AB}, \vec{CD}) = \frac{π}{2} [2 π]$
$\vec{AB} . \vec{CD} = 0$
$(AB) ⊥ (CD)$
$\arg (\frac{d - c}{b - a}) = \frac{π}{2} [π]$

Alignement de trois points.Trois points $A$ , $B$ , et $C$ distincts sont alignés si et seulement si $\vec{AB}$ et $\vec{AC}$ sont colinéaires ce qui s'écrit :

$\exists k \in ℝ$ tel que $\vec{AC} = k \vec{AB}$ .

Les conditions équivalentes sur les affixes des points

A

B

C

sont :

$(\frac{c - a}{b - a}) \in ℝ ⟺ (\frac{c - a}{b - a}) = \bar{(\frac{c - a}{b - a})} ⟺ \arg (\frac{c - a}{b - a}) = 0 [π]$

Droite. Soient $A$ et $B$ deux points distincts du plan complexe d'affixes respectives $a$ et $b$ , $M$ un point du plan d'affixe $z$

$M$ appartient à la droite $(AB) ⟺ (\frac{z - a}{b - a}) \in ℝ ⟺ \arg (\frac{z - a}{b - a}) = 0 [π]$

Exercices.

Montrer que deux vecteurs $\vec{V_{1}}$ et $\vec{V_{2}}$ non nuls, d'affixes respectives $z_{1}$ et $z_{2}$ sont colinéaires si et seulement si : $z_{1} \bar{z_{2}} - \bar{z_{1}} z_{2} = 0$
Montrer que deux vecteurs $\vec{V_{1}}$ et $\vec{V_{2}}$ non nuls, d'affixes respectives $z_{1}$ et $z_{2}$ sont orthogonaux si et seulement si : $z_{1} \bar{z_{2}} + \bar{z_{1}} z_{2} = 0$

\vec{V_{1}}

\vec{V_{2}}

sont colinéaires si et seulement s'il existe

k

dans

ℝ^{*}

, tel que

\vec{V_{1}} = k \vec{V_{2}} ⟺ z_{2} = k z_{1}

\vec{V_{1}}

\vec{V_{2}}

sont orthogonaux si et seulement s'il existe

k

dans

ℝ^{*}

, tel que

z_{2} = i k z_{1}

Exercices sur des triangles.

Triangle isocèle (1)
Triangle rectangle isocèle (2)
Triangle équilatéral

Cercles

Soient $A$ et $B$ deux points distincts d'affixes respectives $a$ et $b$ .

Cercles dans le plan complexe.

Soit $M$ un point du plan d'affixe $m$ . Les deux proposition suivantes sont équivalentes :
- $∣ m - a ∣ = ∣ b - a ∣$
- $M$ est sur le cercle centré en $A$ et passant par $B$ .
Le cercle de centre $Ω$ , d'affixe $ω$ , et de rayon $r$ est l'ensemble des points $M$ d'affixe $z = ω + r e^{i θ}$ , avec $θ$ un réel quelconque.

Exercices. On se place le plan rapporté à un repère orthonormé. Déterminer l'ensemble des points

M

d’affixe

z

vérifiant :

$∣ (1 + i) z - 2 i ∣ = 2$
C'est le cercle de centre $Ω (1, 1)$ et de rayon $r = \sqrt{2}$ .
$ℛ e (\frac{z - 1}{z - i}) = 0$
Le cercle de centre $Ω (\frac{1}{2}, \frac{1}{2})$ et de rayon $r = \frac{\sqrt{2}}{2}$ , privé du point $I$ d'affixe $i$ .
$z + \frac{1}{z}$ est un nombre réel.
C'est la réunion du cercle de centre $O$ , et de rayon $r = 1$ et de l'axe réel privé de l'origine.
$\frac{i z - 4}{z - 4}$ est un nombre réel.
C'est le cercle de centre $Ω (2, - 2)$ et de rayon $r = 2 \sqrt{2}$ , privé du point $(4, 0)$ .

Détermination de lieux

On se place dans le plan rapporté à un repère orthonormé.

Exercices I. Déterminer l'ensemble des points

M

d’affixe

z

vérifiant :

$z + \bar{z} = 1$
- Posons $z = x + i y$ . On a : $z + \bar{z} = 1 \Leftrightarrow 2 ℛ e (z) = 1 \Leftrightarrow x = \frac{1}{2}$ . Le point $M (z)$ est donc sur la droite d'équation $x = \frac{1}{2}$
- Réciproquement, si $M$ est sur la droite d'équation $x = \frac{1}{2}$ , il existe $y$ réel tel que $z = \frac{1}{2} + i y$ . On a alors : $\bar{z} = \frac{1}{2} - i y$ et et $z + \bar{z}$ vaut $1$ .
Le lieu de $M$ est donc la droite d'équation $x = \frac{1}{2}$ .
$z - \bar{z} = i$
- Posons $z = x + i y$ . On a : $z - \bar{z} = i \Leftrightarrow 2 ℐ m (z) = 1 \Leftrightarrow y = \frac{1}{2}$ . Le point $M$ est donc sur la droite d'équation $y = \frac{1}{2}$
- Réciproquement, si $M$ est sur la droite d'équation $y = \frac{1}{2}$ , il existe $x$ réel tel que $z = x + \frac{i}{2}$ . On a alors $\bar{z} = x - \frac{i}{2}$ et $z - \bar{z}$ vaut $i$ .
Le lieu de $M$ est donc la droite d'équation $y = \frac{1}{2}$
$∣ z - a ∣ = ∣ z - b ∣$ où $a$ et $b$ sont des complexes donnés. Solution
On note $A$ le point d'affixe $a$ et $B$ le point d'affixe $b$ . La condition est la traduction géométrique de l'égalité $MA = MB$ . Le lieu de $M$ est donc la médiatrice du segment $[AB]$ . Voir Cours sur la médiatrice .
$∣ z - i ∣ = ∣ i z - i ∣$
On introduit les points $A$ et $B$ , où $A = (1, 0)$ et $B = (0, 1)$ . L'ensemble cherché est la médiatrice du segment $[AB]$ .
$∣ z ∣ < 1$
$∣ z ∣ < 1 \Leftrightarrow OM < 1$ . Le lieu cherché est le disque unité ouvert.
$z + \bar{z} = ∣ z ∣^{2}$
Le lieu est le cercle de centre $(1, 0)$ et de rayon 1.

Exercices II.

Trouver l'ensemble des nombres complexes $z$ tels que les points d'affixe 1, $z$ et $1 + z^{2}$ soient alignés.

Le lieu est la réunion du cercle de centre $A = (1, 0)$ de rayon 1, et de l'axe réel.
Soit $z = x + i y$ un nombre complexe. On pose $Z = \frac{1 - 3 z}{3 - z}$ . Quel est le lieu des points $M$ d'affixe $z$ tel que $Z$ soit réel ? imaginaire pur ?
1. $Z$ est réel : L'ensemble cherché est l'axe des abscisses, privé du point $(3, 0)$ .
2. $Z$ est imaginaire pur : L'ensemble cherché est le cercle de centre $Ω = (\frac{5}{3}, 0)$ et de rayon $\frac{4}{3}$ , privé du point $A = (3, 0)$ .

Exercices III. Il s'agit de reconnaître des zones du plan complexe exprimées en termes de l'argument, le module, la partie réelle et imaginaire. Il y a plusieurs niveaux possibles :

Niveau 0
Niveau 1
Niveau 2

Exercice IV.
Problèmes de maximum ou minimum

Nombres complexes et suites (exercices).

Exercice 1. On considère la suite de nombres complexes

(z_{n})_{n \in ℕ}

, définie par :

z_{0} = 100, z_{n + 1} = \frac{i}{3} z_{n}

, pour tout entier

n

. Dans le plan complexe rapporté à un repère orthonormé direct

(O, \overset{⇀}{u}, \overset{⇀}{v})

, on note

M_{n}

le point d'affixe

z_{n}

Démontrer que, pour tout entier naturel n, les points $O, M_{n} et M_{n + 2}$ sont alignés.
On rappelle qu’un disque de centre $A$ et de rayon $r$ , où $r$ est un nombre réel positif, est l’ensemble des points $M$ du plan vérifiant $AM \leq r$ . Démontrer que, à partir d’un certain rang $n_{0}$ , tous les points $M_{n}$ appartiennent au disque de centre $O$ et de rayon 1.

Calculer $z_{n + 2}$ en fonction de $z_{n}$ et traduire vectoriellement cette égalité.
Calculer $z_{n}$ en fonction de $z_{0}$ ... On trouve $n_{0} = 5$ .

Exercice 2. On considère les nombres complexes

(z_{n})_{n \in ℕ}

définis, pour tout entier

n

, par

z_{0} = 1

z_{n + 1} = (1 + i \frac{\sqrt{3}}{3}) z_{n}

. On note

A_{n}

le point d’affixe

z_{n}

dans un repère orthonormé direct

(O, \overset{⇀}{u}, \overset{⇀}{v})

. L’objet de cet exercice est d’étudier la construction des points

A_{n}

Calculer $z_{1}$ et $z_{2}$ que l’on donnera sous forme exponentielle.
Montrer que, pour tout entier naturel $n$ , $z_{n} = (\frac{2}{\sqrt{3}})^{n} e^{i n \frac{π}{6}}$ . Pour quelles valeurs de $n$ , les points $O$ , $A_{0}$ et $A_{n}$ sont-ils alignés ?
Pour tout entier naturel $n$ , on pose $d_{n} = ∣ z_{n + 1} - z_{n} ∣$ . Interpréter géométriquement $d_{n}$ . Calculer $d_{0}$ , puis montrer que : $z_{n + 2} - z_{n + 1} = (1 + i \frac{\sqrt{3}}{3}) (z_{n + 1} - z_{n})$ . En déduire que la suite $(d_{n})_{n \in ℕ}$ est géométrique puis que, pour tout entier $n$ , $d_{n} = \frac{\sqrt{3}}{3} (\frac{2}{\sqrt{3}})^{n}$
Montrer que pour tout entier naturel $n$ , $∣ z_{n + 1} ∣^{2} = ∣ z_{n} ∣^{2} + d_{n}^{2}$ . En déduire que, pour tout entier naturel n, le triangle ${OA}_{n} A_{n + 1}$ est rectangle en $A_{n}$ . Construire, à la règle non graduée et au compas, le point $A_{5}$ sur une figure et justifier cette construction.

Dans $(1 + i \frac{\sqrt{3}}{3})$ , mettre $\frac{2}{\sqrt{3}}$ en facteur. On trouve : $z_{1} = \frac{2 \sqrt{3}}{3} e^{i \frac{π}{6}}$ . $z_{2} = \frac{4}{3} e^{i \frac{π}{3}}$
$O$ , $A_{0}$ et $A_{n}$ alignés? Écrire une condition sur les arguments. On trouve $n = 6 k$ , avec $k \in ℤ$ .
$(d_{n})_{n \in ℕ}$ est la distance $A_{n} A_{n + 1}$ . C'est une suite géométrique de raison $q = \frac{2}{\sqrt{3}}$ .
Calculer $∣ z_{n + 1} ∣^{2}$ , $∣ z_{n} ∣^{2}$ et $d_{n}^{2}$ , puis vérifier l'égalité demandée.
Pour tracer $A_{1}$ à partir de $A_{0}$ , puisque le triangle $O A_{0} A_{1}$ est rectangle en $A_{0}$ , on trace la perpendiculaire à la droite $O A_{0}$ passant par $A_{0}$ , puis le cercle de centre $A_{0}$ et de rayon $\frac{2}{\sqrt{3}} 0 A_{0}$ . Le point $A_{1}$ est à l'intersection de la droite et du cercle. Et on recommence... on trace la perpendiculaire à la droite $O A_{n}$ passant par $A_{n}$ , puis le cercle de centre $A_{n}$ et de rayon $\frac{2}{\sqrt{3}} 0 A_{n}$ . Le point $A_{n + 1}$ est à l'intersection de la droite et du cercle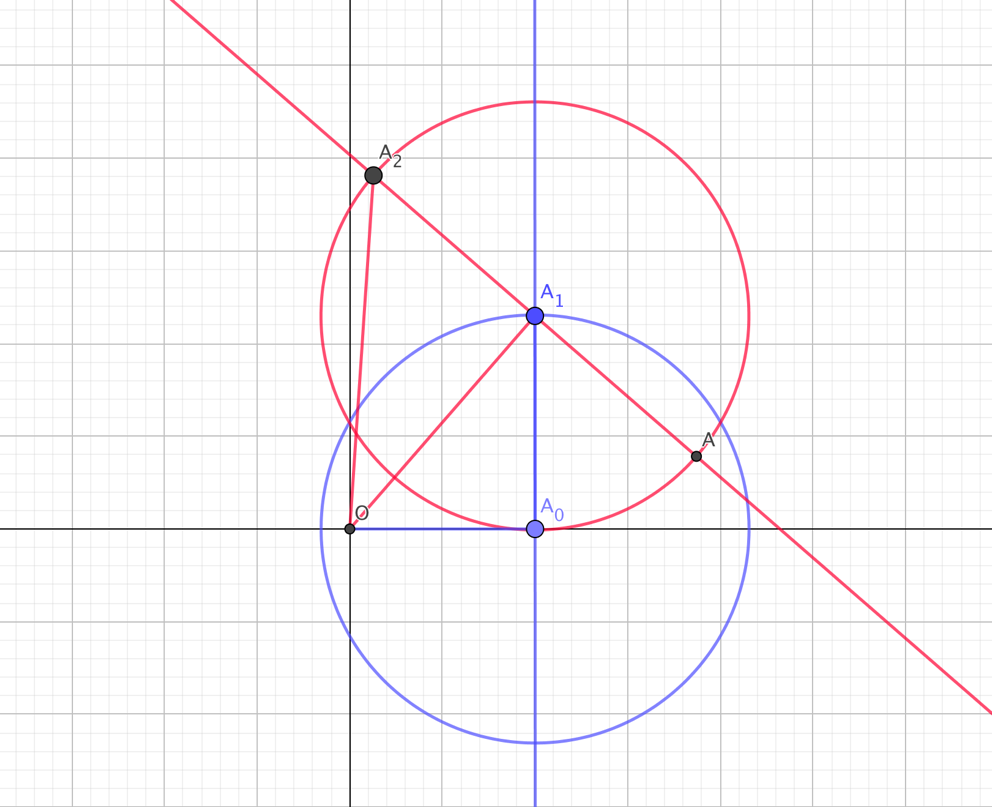

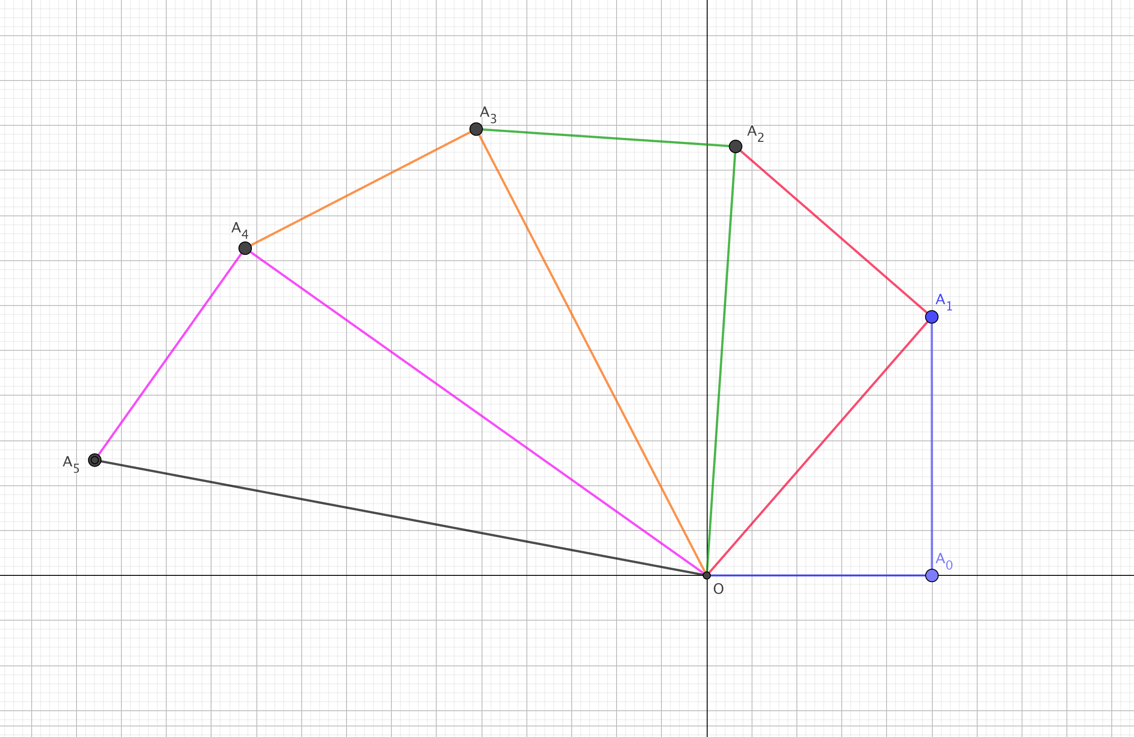
Exercice 3. On considère la suite

z_{n}

définie par

z_{0} = 1 + i

, et pour tout entier naturel non nul

z_{n + 1} = \frac{z_{n} + ∣ z_{n} ∣}{3}

. On pose

z_{n} = a_{n} + i b_{n}

Calculer $z_{1}$ , puis $z_{n + 1}$ en fonction de $a_{n}$ et de $b_{n}$ .
Que peut-on dire de la suite $(b_{n})_{n \in ℕ}$ , quelle est sa limite?
Montrer que, pour tout entier naturel $n$ , $∣ z_{n + 1} ∣ \leq \frac{2 ∣ z_{n} ∣}{3}$ , puis, par récurrence, que $∣ z_{n} ∣ \leq {(\frac{2}{3})}^{n} \sqrt{2}$ . Que peut-on dire de la suite $(∣ z_{n} ∣)_{n \in ℕ}$ ?
Montrer que pour tout entier naturel $n$ , $∣ a_{n} ∣ \leq ∣ z_{n} ∣$ . Conclusion de l'exercice ?

$z_{1} = (\frac{1 + \sqrt{2}}{3}) + \frac{i}{3}$ .
$z_{n + 1} = \frac{a_{n} + \sqrt{a_{n}^{2} + b_{n}^{2}}}{3} + i (\frac{b_{n}}{3})$ . Pour tout $n$ entier naturel $b_{n + 1} = \frac{b_{n}}{3}$ , $(b_{n})_{n \in ℕ}$ est une suite géométrique de raison $\frac{1}{3}$ qui converge donc vers 0.
L'inégalité demandée résulte de l'utilisation de l'inégalité triangulaire, et la récurrence est immédiate. $∣ z_{n} ∣$ est une suite géométrique de raison $\frac{2}{3}$ qui converge donc vers 0.
$∣ a_{n} ∣ = \sqrt{a_{n}^{2}} \leq \sqrt{a_{n}^{2} + b_{n}^{2}} = ∣ z_{n} ∣$ . Les trois suites $a_{n}, b_{n}$ et donc $z_{n}$ sont convergentes et tendent vers 0

cours : forme exponentielle, formules de Moivre et d'Euler, linéarisation, géométrie.
: complex_number,trigonometry,complex_plane,circle,lines, interactive mathematics, interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.