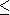Analyse vectorielle
Guide
- Motivation
- Préliminaires
- Champ de vecteurs
- Formes différentielles
- Intégration le long d'une courbe
- Caractérisation des champs de gradients
- Théorème de Green-Riemann
Documents
J. Stewart, Analyse, concepts et contextes, vol. 2, DeBoeck Université (2001)
Motivation
Si est une fonction continue d'un intervalle dans , on définit l'intégrale de à de la fonction : . Il y a deux propriétés de l'intégration que l'on voudrait généraliser lorsqu'on se place dans ou :- Dans le cas où
est positive et
, on peut interpréter
comme une
aire
est l'aire du domaine défini par , :.Ainsi, l'aire du domaine limité par le graphe de la fonction pour et dans [0.7,2.5] et les segments , et est égale àOn a donc relié l'intégrale d'une fonction à une aire, c'est-à-dire à l'intégrale double . Cela s'exprimera plus tard comme le théorème de Green :
- On a la formule d'intégration fondamentale .
Préliminaires
- On peut voir
comme un espace vectoriel sur
 . On appelle alors ses éléments des
vecteurs .
Prenez le aléatoire
ou
On peut additionner des vecteurs ou les multiplier par un scalaire, c'est-à-dire par un réel. On note un élément de soit comme un -uplet soit on l'écrit dans la base canoniquepar exemple pour ,.Pour et , il est fréquent que l'on note les vecteurs de la base canonique par et . Nous utiliserons les trois notations.
. On appelle alors ses éléments des
vecteurs .
Prenez le aléatoire
ou
On peut additionner des vecteurs ou les multiplier par un scalaire, c'est-à-dire par un réel. On note un élément de soit comme un -uplet soit on l'écrit dans la base canoniquepar exemple pour ,.Pour et , il est fréquent que l'on note les vecteurs de la base canonique par et . Nous utiliserons les trois notations.Exercice : espace vectoriel
Tir aux vecteurs - On peut voir
comme un espace affine
formé de
points .
La notation avec un point et un vecteur désigne le point translaté de par le vecteur . Ainsi, dans , si est le point (-0.7, 0.6, 0.1, 1.1) et le vecteur 0.7 e 1 + (0.2 )e 2 + (-1.7 )e 3 + (1.2 )e 4 , est le point (0, 0.8, -1.6, 2.3).
Si , on note .
Un sous-espace affine est le translaté d'un sous-espace vectoriel (appelé sa direction vectorielle). Par exemple , l'ensemble des points de vérifiant est un plan affine. Sa direction vectorielle est d'équation .Exercices sur les équations d'un sous-espace affine
Equaffine et Equaffine . Vous pouvez aussi changer la configuration et faire d'autres types d'exercices. - L'espace vectoriel
est muni d'une norme euclidienne et d'un produit scalaire
:
si et , alors.C'est un espace euclidien .Définition
On peut parler de- vecteurs orthogonaux
- de longueur d'un vecteur :
si v= , ||v||=
- de vecteurs unitaires
- de distance d'un point à une droite, à un plan...
- de produit vectoriel
Quelques exercices sur les distances dans l'espace euclidien
- distance d'une droite à un plan
- distance d'un plan à un plan
- distance d'un point à un plan I
- distance d'un point à un plan II
- distance entre deux droites I
- distance entre deux droites II .
- L'espace affine
est alors muni d'une distance :
et d'une topologie.
Définition
Les boules ouvertes sont les sous-ensembles de de la forme pour un point et un réel positif.
Un sous-ensemble de est dit ouvert si tout point de appartient à une boule ouverte contenue dans . Les boules ouvertes sont des ouverts.
On peut donc définir la continuité d'une fonction d'un ouvert de dans .Exemples
L'ensemble des tels que et n'est pas un ouvert.regarder le point (0,1/2) par exemple
L'ensemble des tels que et est un ouvert .Exercice : topologie ( pas encore)
Champ de vecteurs
- Champ de vecteurs
- Représentation graphique d'un champ
- Exemples de champ
- Le gradient
- Champ de vecteurs associé à une équation différentielle
- Systèmes différentiels
Champ de vecteurs
Définition
Un champ de vecteurs (ou champ vectoriel)
sur
défini sur un domaine
de
est une fonction de
dans
.
Il est dit continu si
est continu,
si
est
(c'est-à-dire continu et
admettant des dérivées partielles continues).
Ainsi, à un point de
, on associe un vecteur
de
.
Exemple
Dans les champs de vecteurs
représentés graphiquement, les longueurs des vecteurs sont souvent modifiés par
un coefficient de proportionnalité pour des raisons esthétiques. Il est souvent
aussi plus facile de représenter le champ de directions associé, c'est-à-dire de
dessiner des vecteurs unitaires représentant les directions du champ en
oubliant son "intensité" c'est-à-dire sa norme.
Voici les deux représentations du champ donné par
.
.
.
Représentation graphique d'un champ
Soit le champ défini par . Voici une représentation de ce champ à droite et la représentation du champ de directions associé à gauche (celui-ci est le champ défini par :|
.
| . |
Exemples de champ
Exemple
-
Le champ de vecteurs tangents à une courbe dans
; il est donc défini sur la courbe et non sur
.
Dessin
- Le champ des vecteurs normaux à une surface dans ; il est défini sur cette surface (attention, on ne peut pas parler du champ de vecteurs tangents à une surface. Pourquoi ?)
- Le gradient
- Les champs associés à des équations différentielles ou des systèmes diffférentiels .
 . Par exemple,
le champ de température est la fonction donnant la température en un point le champ de pression
est la fonction donnant la température en un point.
. Par exemple,
le champ de température est la fonction donnant la température en un point le champ de pression
est la fonction donnant la température en un point.
Exemple
Vous avez rencontré en physique des champs de vitesse
champs de force, des
champs électriques, des
champs magnétiques, des
champs électrostatiques, des champs de vitesse, des
champs gravitationnels. Quelle grandeur physique représente dans chaque cas le
champ ?
Le gradient
Définition
Soit
une fonction de 4 variables. On lui
associe un champ de vecteurs appelé champ de gradient
et noté grad
ou 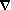 :
avec
.
:
avec
.
En posant
,
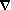 :
:
.
Exercice
Autres notations
- en utilisant la base canonique (
,
,
,
)
=
-
En physique, on utilise la notation suivante :
,
,
ce qui donne les formules suivantes
dansou en mettant les scalaires après les vecteurs contrairement à nos habitudes
dansdans
dans .
Champ de vecteurs associé à une équation différentielle
Soit une fonction sur un ouvert de . On considère une équation différentielle et on lui associe le champ de vecteurs suivant : à un point de , on associe le vecteur unitaire de direction . C'est donc le vecteur . Si est une solution sur un intervalle , on a et le vecteur tangent à la courbe d'équation en un point est colinéaire au champ de vecteurs associé à l'équation différentielle.Exemple
Voici le dessin des directions associés à l'équation différentielle
.
Systèmes différentiels
SoitUne courbe intégrale est, disons,
une courbe paramétrée
qui est
et qui vérifie
En chaque point, la tangente est de direction le champ de vecteurs
.
On les appelle aussi lignes de courant : ce sont par
exemple, les trajectoires d'un objet dont le champ de vitesse est le champ de vecteurs
considéré.
Exemple
.
Le champ associé au système différentiel
est donné par
Formes différentielles
- Rappels sur les formes linéaires
- Formes différentielles
- Lien entre champs de vecteurs et formes différentielles
Rappels sur les formes linéaires
Définition
Une forme linéaire
sur l'espace vectoriel
est une application linéaire de
dans
.
Par exemple, la projection
est une forme linéaire de
, notons-la
.
De même, la projection
est une forme linéaire, notons-la
.
Toute forme linéaire est représentée (dans la base usuelle de ) par une matrice à une ligne et 3 colonnes et on a
.
Ainsi, toute forme linéaire sur
est combinaison linéaire des
.
Exercice
Vérifier que si
est une forme linéaire sur
,
il existe un vecteur
tel que
pour tout vecteur
de
.
Formes différentielles
Commencer par des rappels sur les formes linéaires avant la définition suivante :Définition
Une forme différentielle
 (de degré 1) sur un ouvert
de
est la donnée en chaque point
de
d'une forme linéaire
. En coordonnées,
(de degré 1) sur un ouvert
de
est la donnée en chaque point
de
d'une forme linéaire
. En coordonnées,
Par exemple pour
, cela s'écrit
 (de degré 1) sur un ouvert
de
est la donnée en chaque point
de
d'une forme linéaire
. En coordonnées,
(de degré 1) sur un ouvert
de
est la donnée en chaque point
de
d'une forme linéaire
. En coordonnées,
Exemple des formes différentielles associées à une fonction
Soit
une fonction de
variables. On lui associe la forme différentielle
de degré 1
Par exemple, pour
,
Pour
,
Si
, on obtient
, si
,
on obtient
.
D'où la notation commode
,
et l'expression plus familière
qu'il faut retenir
Pour n=1
La notion (ou notation) si on remplace
par
est la suivante :
à une fonction d'une variable
sur un intervalle
de
,
on associe
.
et lorsqu'il y a
variables,
- un "champ de vecteurs" sur (à valeurs dans ) donné par ;
- une forme différentielle de degré 1 sur notée .
Lien entre champs de vecteurs et formes différentielles
Champs de vecteurs et formes différentielles sont extrêmement liés. Si
.
En posant
, on a alors symboliquement
.
Par exemple, si
est une fonction sur
,
le champ de vecteurs associé à la forme différentielle
est égal à
et on a
Intégration le long d'une courbe
On désire définir l'analogue de avec . Pour cela on remplace le segment [ ] de par une courbe paramétrée de ou de et par une forme différentielle ou par .- Rappels sur les courbes paramétrées
- Intégrale curviligne d'un champ de vecteurs
- Intégrale curviligne d'une forme différentielle
- Flux, travail
- Intégration des champs de gradients
- Exemples
Rappels sur les courbes paramétrées
Définition
Une courbe paramétrée (plane) est une application d'un
intervalle
de
dans
, ce qu'on appelle aussi
fonction vectorielle . Le
paramètre est
, l'image de cette application est formée des points de la courbe.
Autrement dit, si
,
une courbe paramétrée dans
est donnée par
.
On note
l'image de
. Lorsque
est un intervalle fermé borné [a,b], les points extrémités
de
sont les points
et
. La courbe est fermée si
.
On écrit par exemple
|
|
On ne regardera que des courbes par morceaux sur un intervalle fermé, c'est-à-dire telles que les 5 fonctions , , , , soient continues et par morceaux, on appelle une telle courbe un chemin de vers .
Vecteur tangent à une courbe paramétrée
En un point où les sont dérivables et tel que les ) ne soient pas tous nuls, le vecteur vitesse ou vecteur tangent est le vecteur ou encore . Par exemple, pour , la tangente à la courbe en a la représentation paramétriqueLe cercle paramétré par et son vecteur vitesse
1
Exercice sur la droite tangente à une courbe paramétrée.
Changement de paramètres
On peut changer le paramétrage, c'est-à-dire remplacer par où est une bijection d'un intervalle
sur
, continue, dérivable,
à dérivée continue et strictement positive .
Prenons
.
La nouvelle courbe paramétrée est donnée par
,
,
) avec
,
,
pour
. Les points des deux courbes paramétrées
sont les mêmes. Mais le vecteur vitesse n'est pas le même :
est une bijection d'un intervalle
sur
, continue, dérivable,
à dérivée continue et strictement positive .
Prenons
.
La nouvelle courbe paramétrée est donnée par
,
,
) avec
,
,
pour
. Les points des deux courbes paramétrées
sont les mêmes. Mais le vecteur vitesse n'est pas le même :
.
Nous avons supposé que le changement de paramétrage
 est croissant,
ainsi la courbe est "parcourue" dans le même sens de l'extrémité
vers l'extrémité
.
est croissant,
ainsi la courbe est "parcourue" dans le même sens de l'extrémité
vers l'extrémité
.
Choix paramétrés
Longueur d'une courbe et abscisse curviligne
Prenez la dimension aléatoire ouThéorème
Soit
une courbe paramétrée dans
par morceaux d'équations paramétrées
,
,
,
,
,
pour
. La longueur de la courbe est égale à
.
Pour des détails et une démonstration dans le cas de , voir le document Doc Longueur et intégrale curviligne .
Rappelons simplement qu'une abscisse curviligne est un nouveau paramétrage de la courbe par la longueur définie à partir du paramétrage donné par
.
Intégrale curviligne d'un champ de vecteurs
Prenez la dimension aléatoire ouDéfinition
Soit
une courbe paramétrée et
un ouvert contenant
.
Soit
un champ de vecteurs sur
. On définit
l'intégrale curviligne du champ de vecteurs
,
)=
+
le long
de
comme
L'intégrale curviligne de
ne
dépend pas du paramétrage de la courbe
, mais
uniquement de l'image
, ce qui
justifiera la notation
.
Elle ne dépend pas non plus du
changement de coordonnées.
+
)
Indépendance par rapport au paramétrage
Un autre paramétrage de est donné par où est une bijection, dérivable, de dérivée non nulle, croissante. Ce qu'on appelle aussi un difféomorphisme conservant l'orientation de la courbe.
Calculons l'intégrale curviligne de + en utilisant le paramétrage (cas d'un champ de vecteurs sur )
+ )
+ )
+
)
=
Où est cachée l'utilisation de la croissance de
? La formule de changement de variables est
.
L'écriture pour signifie avec . Lorsque est décroissante, l'intervalle est l'intervalle . Pour décroissante, on a donc la formule
.
On déduit de ce calcul que
Théorème
La définition de l'intégrale curviligne a bien un sens, à condition de considérer
le chemin
comme orienté :
"on parcourt la courbe de l'extrémité
vers l'extrémité
".
Changement de coordonnées
Plaçons-nous dans . Soit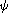 un changement de coordonnées
,
) de
dans un ouvert
: autrement dit, on se donne une application injective
de
sur un ouvert
(donc
bijective de
sur
),
et telle que
le déterminant de
un changement de coordonnées
,
) de
dans un ouvert
: autrement dit, on se donne une application injective
de
sur un ouvert
(donc
bijective de
sur
),
et telle que
le déterminant de
Jac
soit partout non nul sur
. On dit aussi que
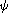 est un
difféomorphisme de
sur
.
est un
difféomorphisme de
sur
.
Soit un champ de vecteurs. On applique le changement de variables , :
=
=
avec
=
Théorème
On a
avec
comme ci-dessus.
Exercice
Que donnent ces formules dans le cas du changement en coordonnées polaires
,
? ne pas chercher à appliquer la formule précédente
mais refaire le calcul dans ce cas particulier.
Qu'en déduit-on lorsque
 est de la forme
avec
une fonction de deux variables ?
est de la forme
avec
une fonction de deux variables ?
 est de la forme
avec
une fonction de deux variables ?
est de la forme
avec
une fonction de deux variables ?
Intégrale curviligne d'une forme différentielle
Définition
Soit
une courbe paramétrée
et
un ouvert de
contenant
.
Soit
une forme différentielle définie sur
. On définit
l'intégrale (curviligne) de la forme
différentielle
 le long du chemin
comme
le long du chemin
comme
Autrement dit, on intègre
 le long du chemin
comme
le long du chemin
comme
 (c(t)) qui est par définition
(c(t)) qui est par définition De même
Définition
Soit
une courbe paramétrée
et
un ouvert
de
contenant
.
Soit  le long du chemin
comme
le long du chemin
comme
Ainsi, si
est le champ de vecteurs associé à
+
+
+
+
une forme différentielle définie sur
. On définit
l'intégrale (curviligne) de la forme
différentielle
 le long du chemin
comme
le long du chemin
comme
+
+
+
+
)
 , l'intégrale curviligne de
, l'intégrale curviligne de  le long de la courbe
est la circulation de
le long de la courbe
.
le long de la courbe
est la circulation de
le long de la courbe
.
L'intégrale curviligne d'une forme différentielle le long d'une courbe est indépendante du changement de paramètre croissant et se comporte bien par changement de coordonnées .
Exercice
Exercice
Flux, travail
L'intégrale curviligne d'un champ de vecteurs le long d'une courbe s'appelle aussi la circulation le long de la courbe. La circulation de ne dépend que de la composante tangentielle de à la courbe.Lorsque le champ vectoriel représente un champ de forces , on parle de travail.
Le flux d'un champ à travers une courbe s'exprime aussi comme une intégrale curviligne, celle du champ . Ainsi, on a
Flux
En remarquant que
"représente"
un vecteur orthogonal à
(vecteur tangent) et que
forment une base directe, on voit que
le flux de
à travers
ne dépend que de la
composante normale de
à la courbe .
Exercice
Intégration des champs de gradients
Théorème
Soit
un champ de vecteurs
et
une courbe paramétrée
d'extrémités
et
. Alors
C'est une généralisation du théorème
.
Démonstration
Démonstration
Faisons la démonstration pour
. On a
(
+
+
+
)
avec
.
D'où la conséquence
Théorème
La circulation d'un champ de gradient le long d'un chemin ne dépend que des
extrémités du chemin.
Exemple
Exemples
Exemple
On considère une attraction proportionnelle à la distance à un point
, appelé centre
d'attraction. Le champ de vecteurs
vérifie
. Ainsi
.
Si
, on a
.
Donc l'intégrale curviligne de
le
long d'un chemin allant d'un point
à un point
ne dépend pas du chemin et vaut
. Autrement dit,
le travail
effectué pour aller de
à
ne dépend pas du chemin.
Exemple
On considère une attraction inversement proportionnelle à la distance à un point
.
Le champ de vecteurs
vérifie donc
Il est défini sur
.
Si
, le gradient de
est égal à
sur
.
L'intégrale curviligne (le travail) de
le long d'un chemin allant de
à
qui ne passe pas par le point
ne dépend que de
et de
et vaut
.
Caractérisation des champs de gradients
- Condition nécessaire
- Condition suffisante pour une boule ouverte
- Remarques
- Théorème général
- Technique d'intégration
- Exercices
- Vers le rotationnel
Condition nécessaire
Prenez la dimension aléatoireSoit un champ de gradient sur un ouvert de (on dit aussi champ dérivant d'un potentiel ou champ conservatif ) sur un ouvert de . Il existe une fonction sur à valeurs dans
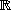 telle que
.
Alors on a
telle que
.
Alors on a
et
par le
théorème de Clairaut-Schwarz
Théorème
Soit
une fonction de
variables
qui est de classe
, c'est-à-dire continue et admettant
des dérivées partielles d'ordre 1 et 2 qui sont continues.
Alors, pour tout indice
et
, on a
Ainsi, si
, on a les égalités de fonctions
.
,
ce qui fait 1
égalité.
On aimerait avoir une réciproque. Mais cela dépend de la forme de l'ouvert.
Condition suffisante pour une boule ouverte
Prenons d'abord pour ouvert une boule ouverte.Théorème
Si
est une boule ouverte de
,
tout champ de vecteurs
vérifiant
les conditions précédentes
pour
et
compris entre 1 et 3
est un champ de gradient.
Démonstration