Géométrie du plan
Géométrie du plan
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Ce document est conçu comme une initiation à la géométrie du plan et une introduction à l'utilisation des groupes. Ce travail mène naturellement à l'étude des frises et des pavages, ce qui est abordé dans un autre document.
Il a été développé au fil d'un cours d'ouverture à l'intention d'étudiants de L1 et L2 comme une promenade dans la géométrie du plan.
IV Groupes et groupes d'isométrie
Document pdf
I De la géométrie aux groupes
Géométrie du plan
→ I De la géométrie aux groupes
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Nous allons commencer par parler de quelques groupes simples.
Géométrie du plan
→ I De la géométrie aux groupes
I-1 Géométrie et géométrie
Géométrie du plan
→
I De la géométrie aux groupes
→ I-1 Géométrie et géométrie
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
- La géométrie des triangles, de droites, des figures : Les grecs calculent avec la géométrie
(construire le nombre dont le carré est 5, trouver le pgcd de deux nombres).Euclide : Couper une droite donnée, de manière que le rectangle compris sous la droite entière et l'un des segments soit égal au carré du segment restant.
SolutionCouper une droite donnée, de manière que le rectangle compris sous la droite entière et l'un des segments, soit égal au carré du segment restant.
Voir la construction
- On prend un segment .
Descartes : Soit l'unité et qu'il faille multiplier par , je n'ai qu'à joindre les points et , puis tirer parallèle à , et est le produit de cette multiplication.
Ou s'il faut tirer la racine carrée de , je lui ajoute en ligne droite , qui est l'unité, et en divisant en deux parties égales au point , du centre , je tire le cercle , puis élevant du point une ligne droite jusques à à angles droits sur ; c'est la racine cherchées
SolutionConstruire la racine carrée d'un nombre représenté par un segment.
Voici le segment de longueur . Ou s'il faut tirer la racine carrée de ,
- La géométrie analytique ou cartésienne : on repère un point par ses coordonnées . Une droite a une équation , on donne des expressions analytiques pour les transformations.
Exemple
Trouver anaytiquement le point d'intersection de la droite passant par et et de la droite d'équation .- La géométrie devient algèbre : on s'intéresse aux structures, aux transformations plutôt qu'aux objets et à leurs propriétés.
Ainsi les dessins sont les mêmes du point de vue de leur groupe de symétrie.
Géométrie du plan → I De la géométrie aux groupes → I-1 Géométrie et géométrie
I-2 Groupes : Introduction
Géométrie du plan
→
I De la géométrie aux groupes
→ I-2 Groupes
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Donnons la définition générale d'un groupe :
I-2-3 Exemple : les matrices d'ordre 2
Un exemple important pour la géométrie (et pour la physique) sont les groupes de symétrie ou groupes d'isométries.
Géométrie du plan
→
I De la géométrie aux groupes
→ I-2 Groupes
I-2-1 Exemples de groupes
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Commençons par des exemples arithmétiques ou numériques : relatifs, réels ou rationnels :
I-2-1-1 Les nombres
Soit
l'ensemble des nombres relatifs ou
l'ensemble des nombres rationnels
ou
l'ensemble des nombres réels. Pour tous éléments
,
,
de
- ;
- ;
- ;
- il existe un élément tel que .
I-2-1-2 Les racines de l'unité
Soit n un entier
. Soit
l'ensemble des nombres complexes
pour
. C'est aussi l'ensemble des nombres complexes
vérifiant
.
Il vérifie pour
dans
et
et
entiers
- ;
- ;
- ;
- .
- ;
- ;
- ;
- il existe un élément tel que .
Exercice
Dessiner
,
,
,
... Pour
,
prendre
et repérer successivement les produits
pour
:
,
,
, ...
Exercice
Racines de l'unité et puissances
Sous-groupe de racines de l'unité
Sous-groupe de racines de l'unité II
Sous-groupe de racines de l'unité III
Sous-groupe de racines de l'unité
Sous-groupe de racines de l'unité II
Sous-groupe de racines de l'unité III
Des manipulations sur trois boules permettent aussi de trouver un groupe :
I-2-1-3 Permutations
(Lire la BD de Stewart : Ah les beaux groupes - les chroniques de Rose Polymath (Belin))
On a trois boules alignées. On peut ne pas changer leur ordre. C'est l'opération identité . On peut changer leur ordre en échangant les deux premières (opération ), en faisant tourner les trois dernières (opération ) et en effectuant ces opérations successivement. Donner le résultat comme un tableau : si une opération nouvelle apparaît, lui donner un nom ( , ...) et la rajouter.
On appelle ces opérations des permutations
de l'ensemble des trois boules.
On note la permutation qui transforme 1, 2, 3 en , , . Par exemple, est la permutation qui transforme 1, 2, 3 en 2, 3, 1.
(Lire la BD de Stewart : Ah les beaux groupes - les chroniques de Rose Polymath (Belin))
On a trois boules alignées. On peut ne pas changer leur ordre. C'est l'opération identité . On peut changer leur ordre en échangant les deux premières (opération ), en faisant tourner les trois dernières (opération ) et en effectuant ces opérations successivement. Donner le résultat comme un tableau : si une opération nouvelle apparaît, lui donner un nom ( , ...) et la rajouter.
| ... | |||||||||
| ... | |||||||||
On note la permutation qui transforme 1, 2, 3 en , , . Par exemple, est la permutation qui transforme 1, 2, 3 en 2, 3, 1.
Exercice
Permutations I
Permutations II
Permutations III
Permutations II
Permutations III
Enfin, voici un exemple de groupe formé d'applications.
I-2-2 Groupes : définition
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
On se donne
un ensemble et une application
dans
qu'on va noter
( on parle de loi, d'opération):
vérifiant
pour tous éléments
,
,
de
L'ensemble muni de la loi est appelé un groupe.
-
loi interne
-
associativité
;
-
élément neutre
il existe un élément tel que ;
-
inverse
il existe un élément tel que .
L'ensemble muni de la loi est appelé un groupe.
Définition
Si a un nombre fini d'éléments, on représente la loi sous la forme d'un tableau.
Exercice
Prenons
. Remplissez les deux tableaux selon les règles
d'addition et de multiplication. Sont-ils la table d'un groupe ?
Si oui, quel est l'élément neutre ?
+ | pair | impair |
| pair | ||
| impair |
 | pair | impair |
| pair | ||
| impair |
Exercice
Prenons
:
On définit
. Compléter le tableau
en appelant
,
,
,
.
Est-il commutatif ?
I-2-3 Exemple : les matrices d'ordre 2
Géométrie du plan
→
I De la géométrie aux groupes
→
I-2 Groupes
→ I-2-3 Exemple : les matrices d'ordre 2
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Une matrice carrée de taille
est un tableau à
lignes et
colonnes.
Nous allons regarder le cas où
. Une matrice carrée
de taille 2 s'écrit alors
où
,
,
et
sont les coefficients.
On définit des opérations sur l'ensemble des matrices d'ordre 2 à coefficients réels :
Addition :
Multiplication :
On définit des opérations sur l'ensemble des matrices d'ordre 2 à coefficients réels :
Addition :
Exercice
Démontrer que
muni de cette opération est un groupe commutatif.
Multiplication :
Exercice
Effectuer le produit
Exercice
Produit de matrices
Inverse de matrices
Équation de matrices
Exercice
Lesquelles des propriétés de groupe sont vérifiées pour l'opération multiplication
? Que faut-il rajouter comme condition pour avoir une opération de groupe ?
Géométrie du plan
→
I De la géométrie aux groupes
→
I-2 Groupes
→ I-2-3 Exemple : les matrices d'ordre 2
I-2-4 Groupe de symétrie : un premier contact
Géométrie du plan
→
I De la géométrie aux groupes
→
I-2 Groupes
→ I-2-4 Groupe de symétrie : un premier contact
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
On appelle isométrie une application du plan (ou de l'espace) conservant les
distances :
pour tous points
et
.
On note
l'ensemble des isométries du plan.Quelques exemples dans le plan :
- l'identité ;
- les rotations ;
- les réflexions par rapport à une droite ;
- les symétries centrales par rapport à un point.
Exercice [Le rectangle]
Chercher les isométries du type précédent qui conservent un rectangle
(quelconque,
c'est-à-dire qui n'est pas un carré).
Suite
Soit
le centre de gravité du rectangle, c'est-à-dire l'intersection
des diagonales. On trouve
On peut composer ces transformations. En obtient-on d'autres ?
Le groupe est-il commutatif ?
Comment chacune des ces transformations permutent-elles
les sommets
,
,
,
?
On a ainsi défini une application du groupe de symétrie du rectangle dans le groupe des permutations des quatre sommets , , et .
- l'identité
- les réflexions par rapport à chacune des médiatrices des côtés , ;
On peut composer ces transformations. En obtient-on d'autres ?
|
| ||||
|
| A | B | C | D |
|
| ||||
On a ainsi défini une application du groupe de symétrie du rectangle dans le groupe des permutations des quatre sommets , , et .
Exercice [Le triangle équilatéral]
Suite
Soit
le centre de gravité du triangle. Il doit être fixe (pourquoi ?). On trouve
On peut composer ces transformations. En obtient-on d'autres ?
L'ensemble est un groupe. On peut faire quelques remarques sur le tableau une fois rempli : que remarquez-vous sur chaque ligne ou sur chaque colonne ?
Comment chacune des ces transformations permutent-elles les sommets , , ?
Vérifier qu'on définit ainsi une application du groupe de symétrie du triangle dans le
groupe des permutations des trois sommets
,
et
.
- l'identité
- les réflexions par rapport à chacune des médiatrices , , ;
- les rotations d'angle , , et de centre .
On peut composer ces transformations. En obtient-on d'autres ?
|
| ||||||
|
| ||||||
L'ensemble est un groupe. On peut faire quelques remarques sur le tableau une fois rempli : que remarquez-vous sur chaque ligne ou sur chaque colonne ?
Comment chacune des ces transformations permutent-elles les sommets , , ?
|
| A | B | C |
|
| |||
Exercice [Autres figures]
Géométrie du plan
→
I De la géométrie aux groupes
→
I-2 Groupes
→ I-2-4 Groupe de symétrie : un premier contact
I-2-5 Groupe de symétrie : définition
Géométrie du plan
→
I De la géométrie aux groupes
→
I-2 Groupes
→ I-2-5 Groupe de symétrie : définition
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Soient
un ensemble de points dans le plan. L'ensemble des isométries conservant
F est un groupe et est appelé groupe de symétrie de
ou groupe d'isométries. On le note ici
.
Si ce groupe est fini, on appelle ordre le nombre de ses éléments.
Exercice
Dessiner une figure ayant la symétrie du rectangle, du triangle équilatéral (et qui
n'en soit pas un), c'est-à-dire telle que son groupe de symétrie soit celui du rectangle ou du triangle
équilatéral.
Exercice
Trouver le groupe de symétrie des lettres de l'alphabet et écrire son ordre dans le
tableau (on ne tiendra pas compte des grosseurs de trait légèrement différentes ...).
A | B | C | D | E | F | G | H | I | J | K | L | M |
N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
Géométrie du plan
→
I De la géométrie aux groupes
→
I-2 Groupes
→ I-2-5 Groupe de symétrie : définition
I-3 Rappels : Le plan complexe
Géométrie du plan
→
I De la géométrie aux groupes
→ I-3 Rappels : Le plan complexe
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Donnons quelques rappels sur le
plan complexe et les isométries dans le plan complexe.
- Un nombre complexe s'écrit où et sont des réels : est la partie réelle de , est la partie imaginaire de .
- Le conjugué de est .
- Le module de est .
- Tout nombre complexe de module 1 s'écrit avec unique modulo : c'est l'argument de (on peut par exemple prendre entre 0 et ). On pose .
- Tout nombre complexe non nul s'écrit de manière unique avec et l'argument de . On représente un point du plan par son affixe :
Géométrie du plan
→
I De la géométrie aux groupes
→ I-3 Rappels : Le plan complexe
I-3-1 Quelques similitudes
Géométrie du plan
→
I De la géométrie aux groupes
→
I-3 Rappels : Le plan complexe
→ I-3-1 Quelques similitudes
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Soient
,
,
,
.
Représenter chacune de ces transformations.
- L'application
est une rotation de centre
(ou
) et d'angle
:
- L'application
est une
translation :
- L'application
est une
homothétie de centre
(ou
) et de rapport
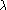 :
:
Représenter chacune de ces transformations.
Géométrie du plan
→
I De la géométrie aux groupes
→
I-3 Rappels : Le plan complexe
→ I-3-1 Quelques similitudes
I-3-2 Exercices
Géométrie du plan
→
I De la géométrie aux groupes
→
I-3 Rappels : Le plan complexe
→ I-3-2 Exercices
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Calculer le composé de deux transformations décrites précédemment.
Donner leur nature.
Trouver à partir de ces résultats des groupes (pour la loi de composition des transformations).
On dit qu'une transformation
conserve les angles si pour tous points
,
,
,
les angles de droite
et
sont égaux.Exercice
Soit l'application
avec
et
des complexes.
A quelle condition
cette transformation est-elle une isométrie, c'est-à-dire conserve-t-elle les distances ?
Conserve-t-elle
les angles ? Discuter suivant
et
et déterminer sa nature géométrique.
Exercice
Soit l'application
avec
et
des complexes.
A quelle condition
cette transformation est-elle une isométrie, c'est-à-dire conserve-t-elle les distances ? Conserve-t-elle
les angles ? Représenter le cas particulier
. A quoi correspond la transformation
?
Une similitude conserve les rapports de distance : il existe une constante telle que
Exercice
En plaçant bien un triangle équilatéral dans le plan complexe (par exemple,
son centre de gravité en
et un de ses sommets en
), expliciter les similitudes complexes
qui le laissent invariant.
Exercice
- Triangle équilatéral
- Tir de rotation
- Billard circulaire (1 rebond)
- Billard circulaire (2 rebonds)
- Billard elliptique
- Triangles, rectangles et similitudes
- Composition de similitudes
- Figures et similitudes
-
Nature des transformations z -> az+b
Exercice
Composés de symétries centrales
Géométrie du plan
→
I De la géométrie aux groupes
→
I-3 Rappels : Le plan complexe
→ I-3-2 Exercices
I-3-3 Indication pour trouver la nature géométrique
Géométrie du plan
→
I De la géométrie aux groupes
→
I-3 Rappels : Le plan complexe
→ I-3-3 Indication pour trouver la nature géométrique
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Pour trouver la nature géométrique d'une application du plan complexe de la forme
- Si , : il s'agit d'une translation de vecteur représenté par .
- Si
, l'équation
en
a une solution
et la transformation
a donc un
point fixe
d'affixe
. On peut alors écrire
- Si est réel, est une homothétie de rapport et de centre .
- Si est un nombre complexe de module 1 et d'argument modulo , est une rotation d'angle et de centre .
- Si est un complexe de module et d'argument modulo , est une similitude d'angle , de centre et de rapport . Dans ce cas, est le composé d'une homothétie et d'une rotation.
Géométrie du plan
→
I De la géométrie aux groupes
→
I-3 Rappels : Le plan complexe
→ I-3-3 Indication pour trouver la nature géométrique
II Géométrie du plan
Géométrie du plan
→ II Géométrie du plan
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Donnons d'abord quelques notions de base sur le plan vectoriel en s'appuyant sur le programme de terminale.
Voici quelques théorèmes dans le plan affine. Faites vous-même un dessin (et même plusieurs) pour comprendre l'énoncé de chacun de ces théorèmes.
Et le plan est plus riche si on introduit une structure euclidienne, c'est-à-dire une distance, une norme, un produit scalaire ... (d'ailleurs, dans le plan complexe, cela existe aussi).
Géométrie du plan
→ II Géométrie du plan
II-1 Le plan vectoriel
Géométrie du plan
→
II Géométrie du plan
→ II-1 Le plan vectoriel
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Le plan vectoriel est
. C'est l'ensemble des couples de nombres réels
.
On appelle ses éléments des vecteurs. Par exemple, le vecteur nul est
. On note
,
.
On peut additionner des vecteurs et multiplier un vecteur par un nombre réel.
II-1-1 Définitions et propriétés
Géométrie du plan
→
II Géométrie du plan
→ II-1 Le plan vectoriel
II-1-1 Définitions et propriétés
Géométrie du plan
→
II Géométrie du plan
→
II-1 Le plan vectoriel
→ II-1-1 Définitions et propriétés
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
L'addition dans le plan vectoriel est une loi de groupe commutatif : pour tous
vecteurs
,
et
du plan,
La multiplication d'un vecteur par un réel est compatible avec l'addition : pour tous vecteurs et du plan et tous réels et ,
- (associativité) ;
- (élément neutre) ;
- (opposé) ;
- (commutativité) .
La multiplication d'un vecteur par un réel est compatible avec l'addition : pour tous vecteurs et du plan et tous réels et ,
- ;
- (distributivité) ;
- (distributivité) ;
- (élément absorbant) ;
Géométrie du plan
→
II Géométrie du plan
→
II-1 Le plan vectoriel
→ II-1-1 Définitions et propriétés
II-1-2 Droites
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Une droite vectorielle est une partie
du plan formée des multiples
,
d'un vecteur non nul
. On dit que
est une base de
. Tout autre vecteur non nul
appartenant à
en est une base.
Si , alors . On dit que est une équation de la droite . Si , on peut mettre cette équation sous la forme
ou encore
.
Le
nombre
est la pente (coefficient directeur) de la droite.
Le vecteur nul appartient à toutes les droites
vectorielles.II-1-3 Indépendance et colinéarité
Géométrie du plan
→
II Géométrie du plan
→
II-1 Le plan vectoriel
→ II-1-3 Indépendance et colinéarité
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Pour que deux vecteurs soient colinéaires, il faut et il suffit qu'ils appartiennent à la même droite.
Définition
Propriétés
Soient deux vecteurs
et
. Les propriétés suivantes
sont équivalentes :
Trouver
et
revient à résoudre un système linéaire.- et sont linéairement indépendants ;
- ;
- tout vecteur s'écrit de manière unique avec et dans .
Géométrie du plan
→
II Géométrie du plan
→
II-1 Le plan vectoriel
→ II-1-3 Indépendance et colinéarité
II-1-4 Bases
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Une base de
est un couple
de vecteurs linéairement indépendants.
Si
est un vecteur, les réels
et
tels que
sont
appelés les coordonnées/composantes
de
dans la base
.
Par exemple, les composantes de dans la base sont et .
Soient et les composantes de et dans la base . Alors, les composantes du vecteur dans la base sont , c'est-à-dire sous forme matricielle et en colonne :
Propriétés
Soient
une base du plan vectoriel,
et
deux vecteurs de composantes
respectives
et
dans la base
.
- Les vecteurs et sont colinéaires si et seulement si .
- L'ensemble des vecteurs dont les composantes dans la base vérifient est une droite vectorielle.
Exercice
Changement de base
Exercice
Soit
un nombre réel. On considère les vecteurs
et
.
- A quelle condition sur le couple est-il une base du plan vectoriel ?
- Donner les coordonnées du vecteur dans la base en fonction des coordonnées dans la base usuelle.
Exercice
- Trouver l'intersection de 2 droites
- Trouver l'intersection de 2 droites II
- Trouver l'intersection de 2 droites II
- Fonctions linéaires/affines et droites
- Projections
- Tir aux vecteurs
II-2 Le plan affine
Géométrie du plan
→
II Géométrie du plan
→ II-2 Le plan affine
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Le plan affine est toujours mais vu un peu différemment (on le note ici ). D'abord, on va appeler ses éléments des points. Un point du plan est donc encore un couple de réels. Le point a pour abscisse et pour ordonnée . On appelle bipoint un couple de points.
Géométrie du plan
→
II Géométrie du plan
→ II-2 Le plan affine
II-2-1 Translations
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Remarquons qu'on vient de définir la notation où est un point et un vecteur.
Propriétés
- est une bijection de dans ;
- ;
- .
Propriétés
- Pour tout bipoint
, il existe un unique vecteur
tel que
.
On le note aussi
. On a donc la relation
- {Relation de Chasles} Pour tous points
,
,
de
, on a la relation
- Pour tout point du plan et tout vecteur , il existe un unique point tel que .
La troisième affirmation est la bijectivité de la translation .
II-2-2 Repères du plan
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Un repère (affine) du plan est un triplet
formé d'un point du plan affine
et de deux vecteurs
formant une base du plan vectoriel. Les coordonnées
de
dans le repère
sont les composantes du vecteur
dans la base
.
Ainsi, tout point
de
s'écrit de manière unique
et
sont les coordonnées de
M dans le repère affine
.
Exemple
Soit
,
,
. Écrire les coordonnées du point
dans le repère
.
Exercice
Changement de repère
II-2-3 Droites affines
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Une droite affine
est une partie du plan affine telle que pour tout
,
l'ensemble des vecteurs
pour
soit une droite vectorielle.
Ce qu'on peut dire d'autres manières :
- ;
- est le translaté par le vecteur d'une droite vectorielle de base ; la droite est appelée direction de . La direction de est aussi l'ensemble des vecteurs pour et des points de . Un vecteur directeur de est une base de la direction de .
Définition
Trois points
,
et
du plan affine
sont alignés s'ils appartiennent à une
même droite, c'est-à-dire si les vecteurs
et
sont colinéaires.
L'ensemble des points alignés avec deux points distincts du plan forme une droite. C'est la droite passant par ces deux points. Toute droite affine est aussi l'ensemble des points vérifiant une équation . Sa direction est d'équation .
Remarque
On a donc plusieurs manières de se donner une droite et de la représenter. Il est important de
savoir passer d'une "représentation à l'autre" et de savoir utiliser la plus adéquate pour résoudre des
problèmes.
Ainsi, pour se donner une droite, on peut
- se donner un point et un vecteur non nul ;
- se donner deux points distincts et ;
- écrire l'ensemble des points de la droite comme les points
tels que
soit colinéaire
à
pour un point
et un vecteur
non nul :
- écrire l'ensemble des points de la droite comme les points
barycentres de deux points
et
distincts :
- écrire l'ensemble des coordonnées des points de la droite :
- donner une relation entre les coordonnées
vérifiées par les coordonnées des points de
la droite et uniquement par eux.
Les vecteurs
et
sont des vecteurs directeurs. Le coefficient directeur (pente)
de la droite affine
est la pente de sa direction. C'est donc
si
avec
non nul et
 si
.
si
.
Exercice
Donner plusieurs manières de représenter la droite passant par les deux points
et
.
II-2-4 Incidence
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Deux droites affines sont parallèles si elles ont même direction.
Propriétés
- Pour que deux droites et soient parallèles, il faut et il suffit qu'il existe une translation telle que .
- Si est une droite affine et un point du plan, il existe une unique droite affine parallèle à et passant par (c'est-à-dire telle que ) : est l'image de la direction de par la translation de vecteur . Si est un point de , c'est aussi l'image de par la translation de vecteur .
Définition
Propriétés
Deux droites parallèles
et
sont soit disjointes
(
), soit confondues (
).
Propriétés
Deux droites sont soit parallèles, soit sécantes (
avec
un point
du plan).
Corollaire
Deux droites
d'équation
et
d'équation
sont parallèles si
. Elles sont sécantes si et seulement si
.
Exercice
- Parmi les points suivants, lesquels sont alignés ?
,
,
,
,
- Déterminer l'intersection de et de .
Exercice
- Parmi les droites suivantes, déterminer lesquelles
sont parallèles, lesquelles sont concourantes et leurs points
d'intersection :
, , , ,
- Donner l'équation générale des droites passant par
.
- Déterminer l'équation de la parallèle
à
passant par
.
Exercice
Soit
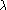 un réel non nul.
un réel non nul.
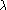 un réel non nul.
un réel non nul.- Donner l'équation de la droite
passant par les
points
et
.
- Soit
un point du plan. Donner tous les
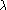 tels que
appartient à
.
tels que
appartient à
.
- Décrire
.
Exercice
On considère les points
,
,
.
- Donner les coordonnées des points et dans le repère .
- Donner une équation dans le repère usuel de la droite
 d'équation
dans le repère
.
d'équation
dans le repère
.
Exercice
Reconnaître rapidement des droites parallèles ou perpendiculaires
II-2-5 Barycentres de points
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Soient
un entier,
, ...,
points et
, ... ,
des réels tels que
.
Le barycentre des points pondérés
, ...,
est l'unique point
du plan tel que
Si
est un point du plan, il vérifie :
Le milieu du segment est l'unique point tel que . Les coordonnées de , et vérifient
Propriétés
Si
et
sont deux points distincts, la droite
est l'ensemble des barycentres
de
et
.
Exercice
Décrire l'ensemble des points du segment
.
Propriétés [Associativité du barycentre]
Si
et si
est le barycentre de
,
, le barycentre de
,
,
, ...,
est égal au barycentre de
,
, ...,
s'ils existent.
Quand les poids , ..., sont tous égaux, on appelle le barycentre l'isobarycentre ou centre de gravité.
Exemple [ Barycentre de deux points ]
Exercice
Placer le barycentre de points
II-2-6 Polygones
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Un triangle est un triplet
de points. Si les points
,
,
sont
alignés ou confondus, on dit que
est dégénéré.
Supposons
non dégénéré. Les points
,
,
sont les sommets, les droites
,
,
sont les côtés. Le côté
est opposé à
. Soient
,
et
les
milieux respectifs des côtés opposés
à
,
et
. Les droites
,
,
sont les médianes du triangle.
Elles passent par le centre de
gravité
de
.
Définition
Pour qu'un quadruplet (quadrilatère) soit un parallèlogramme, il faut et il suffit que les segments et aient même milieu.Définition
L'enveloppe convexe
d'un ensemble de points est l'ensemble des barycentres
à coefficients positifs (une fois normalisé pour que la somme des poids soit positive).
Le segment
est l'enveloppe convexe de
et
.
Définition
Propriétés
L'enveloppe convexe d'un ensemble de points est le plus petit convexe contenant
ses points.
II-2-7 Exercices
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Tracer les trois droites d'équation
,
,
.
Caractériser chacune des régions déterminées par ces droites à l'aide de leurs équations.
Exercice
Soient
,
et
trois points du plan et
,
,
trois réels non nuls tels que les barycentres suivants existent :
- Montrer que , , sont concourantes en .
- Montrer que
,
et
passent respectivement
par
,
et
.
Solution
- Montrons que est sur la droite . Par associativité du barycentre, est le barycentre de , , , et donc de , . Donc est sur la droite . De même pour les autres.
- Soit le barycentre de et . Alors, est le barycentre de et de , est le barycentre de et de . Donc , et sont alignés.
Exercice
Tracer un triangle non dégénéré et les droites prolongeant les côtés
du triangle. Caractériser chacune
des sept régions obtenus en termes de barycentres des trois sommets du triangle.
(On peut commencer par
les régions déterminées par une droite.)
Exercice
Régions
Exercice
- Barycentre de trois points
- Barycentre et côtés d'un triangle
- Barycentre : lequel ?
Exercice
- Tir de gravité I
- Tir de gravité II
- Tir de gravité III
- Coordonnées barycentriques
- Zones barycentriques
- Associativité du barycentre
II-3 Le plan affine avancé
Géométrie du plan
→
II Géométrie du plan
→ II-3 Le plan affine avancé
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Géométrie du plan
→
II Géométrie du plan
→ II-3 Le plan affine avancé
II-3-1 Théorème de Thalès
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Théorème [Thalès]
Soient
,
,
trois points alignés et
,
deux points alignés avec
tels que
et
ne soient pas colinéaires. Alors :
Propriétés [Conséquence]
Soient
,
et
trois points distincts du plan non alignés.
Soient
et
les
milieux respectifs de
et de
. Alors, les droites
et
sont parallèles.
Il y a de nombreuses autres formulations du théorème de Thalès, par exemple :
Propriétés
Soient
,
,
trois points alignés et
,
deux points alignés avec
tels que
,
,
ne soient pas alignés. Alors, si
est
le barycentre de
et
,
est le barycentre de
et
si et seulement
si les droites
et
sont parallèles.
II-3-2 Théorème de Ceva
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Théorème [Ceva]
Soit un triangle
et
,
et
des points situés respectivement sur les
côtés opposés à
,
et
. Les droites
,
et
sont concourantes
si et seulement si
Démonstration
Exemple
Soient
et
deux points. Si
est barycentre de
et de
,
est égal à
. Cela fait un pont entre les barycentres et
le théorème de Ceva.
Exercice
Barycentre et théorème de Ceva
Théorème [Médianes]
- Les médianes d'un triangle sont concourantes.
- Les médianes d'un triangle partagent celui-ci en six petits triangles d'aires égales.
- Les hauteurs d'un triangle sont concourantes.
II-3-3 Théorème de Ménélaüs
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Théorème [Ménélaüs]
Soit un triangle
et
,
et
des points situés respectivement sur les
droites
,
et
. Les points
,
et
sont alignés
si et seulement si
II-3-4 Birapport
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Rappelons que si , sont deux points distincts, le rapport détermine la position d'un point de la droite par rapport à et .
Définition
Théorème
Soit
le birapport des quatre points alignés
,
,
,
et
un point distinct
et non aligné avec les quatre points.
Alors
Démonstration
On note
 la droite sur laquelle se trouve les points
,
,
,
.
Soit
le projeté orthognal de
sur la droite
la droite sur laquelle se trouve les points
,
,
,
.
Soit
le projeté orthognal de
sur la droite
 .
.
L'aire du triangle est égale à .
L'aire du triangle est égale à .
L'aire du triangle est égale à .
L'aire du triangle est égale à .
Ce qui montre facilement la première formule.
Pour la deuxième formule. on calcule l'aire des triangles précédents en choisissant une autre base :
etc, ce qui permet de démontrer la formule au signe près.
Regardons maintenant le signe.
Le point est d'un côté de la droite ! On choisit une orientation pour tourner autour du point (le résultat ne dépend pas du choix car il y a 4 termes). Cela donne une orientation de la droite pour laquelle le sinus de
est positif si et seulement si
est positif pour deux points
et
de la droite
pour laquelle le sinus de
est positif si et seulement si
est positif pour deux points
et
de la droite
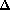 .
.
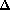 la droite sur laquelle se trouve les points
,
,
,
.
Soit
le projeté orthognal de
sur la droite
la droite sur laquelle se trouve les points
,
,
,
.
Soit
le projeté orthognal de
sur la droite
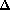 .
.
L'aire du triangle est égale à .
L'aire du triangle est égale à .
L'aire du triangle est égale à .
L'aire du triangle est égale à .
Ce qui montre facilement la première formule.
Pour la deuxième formule. on calcule l'aire des triangles précédents en choisissant une autre base :
Regardons maintenant le signe.
Le point est d'un côté de la droite ! On choisit une orientation pour tourner autour du point (le résultat ne dépend pas du choix car il y a 4 termes). Cela donne une orientation de la droite
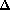 pour laquelle le sinus de
est positif si et seulement si
est positif pour deux points
et
de la droite
pour laquelle le sinus de
est positif si et seulement si
est positif pour deux points
et
de la droite
 .
.
Corollaire
Le nombre
ne dépend que des
droites
,
,
et
et non de la sécante :
On le note aussi
C'est le birapport des quatre droites.
Soit un autre point, on a
Soit un autre point, on a
Exercice
Sur le birapport de quatre points
Conjugué harmonique
Conjugué harmonique
II-3-5 Théorème de Pappus
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Théorème [Pappus]
Soient
,
,
trois points alignés situés sur une droite
,
Soient
,
,
trois autres points alignés situés sur une autre droite. Les trois
points
,
et
définis respectivement comme l'intersection de
et de
,
l'intersection de
et de
et
l'intersection de
et de
sont alignés.
Démonstration
Figure interactive (JSXGraph)
II-3-6 Théorème de Desargues
Géométrie du plan
→
II Géométrie du plan
→
II-3 Le plan affine avancé
→ II-3-6 Théorème de Desargues
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Théorème [Desargues]
Soient
,
,
trois droites concourantes. Si
et
sont sécantes en
, si
et
sont sécantes en
,
et
sont sécantes en
,
alors
,
et
sont alignés.
Une autre formulation est :
Théorème
Si les droites joignant les sommets homologues de deux triangles sont concourantes,
les points d'intersection de leurs côtés homologus sont alignés et réciproquement.
Le théorème de Desargues est en fait un théorème dans l'espace que l'on peut projeter
sur un plan.Ce fait est bien mis en évidence par l'applet suivante : Le point 1 (boule rouge) est l'intersection de trois droites concourantes de l'espace. Les triangles "homologues" sont les triangles 2, 3, 4 (boules violettes) et 5, 6, 7 (boules bleues). Les droites des côtés du triangle violet sont dans le plan de ce triangle et coupent les droites des côtés du triangle bleu selon l'intersection des deux plans qui est une droite (en général : oublions les cas de parallèlisme ...)
Mais pourquoi les droites des côtés homologues se coupent-elles ? Deux droites de l'espace ne se coupent pas en général (même si elles ne sont pas parallèles). Mais ici, ces droites sont dans un même plan : le plan contenant les deux droites concourantes au point rouge et portant respectivement un des deux sommets du côté et le sommet homologue. Et deux droites d'un plan sont sécantes ou parallèles.
conclusion
http://wims.univ-savoie.fr/wims/wims.cgi?session=../tmp/robot.1&+cmd=getfile&+special_parm=file_31.spt, http://wims.univ-savoie.fr/wims/wims.cgi?session=../tmp/robot.1&+cmd=getfile&+special_parm=file_31.xyz
Géométrie du plan
→
II Géométrie du plan
→
II-3 Le plan affine avancé
→ II-3-6 Théorème de Desargues
II-3-7 Exercice : Droite de Newton
Géométrie du plan
→
II Géométrie du plan
→
II-3 Le plan affine avancé
→ II-3-7 Exercice : Droite de Newton
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Soit
un triangle non dégénéré et
une droite
sécante aux côtés du triangle respectivement en
,
et
. Montrer
que les milieux
,
, et
de
,
et
sont alignés.
Construction
Soient trois points , et non alignés.
Géométrie du plan
→
II Géométrie du plan
→
II-3 Le plan affine avancé
→ II-3-7 Exercice : Droite de Newton
II-3-8 Un autre exercice
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Faire bouger les points de manière à les placer dans une situation non dégénérée. Que constatez-vous ? Conjecturer le sujet de l'exercice et le démontrer.
II-4 Le plan euclidien
Géométrie du plan
→
II Géométrie du plan
→ II-4 Le plan euclidien
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Le plan vectoriel euclidien est le plan vectoriel ou affine avec un produit scalaire :
Définition
II-4-1 Propriétés du produit scalaire
II-4-3 Version affine : la distance
Géométrie du plan
→
II Géométrie du plan
→ II-4 Le plan euclidien
II-4-1 Propriétés du produit scalaire
Géométrie du plan
→
II Géométrie du plan
→
II-4 Le plan euclidien
→ II-4-1 Propriétés du produit scalaire
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
Soient
,
et
trois vecteurs et
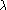 et
et
 des réels. Le produit scalaire vérifie les
propriétés suivantes :
des réels. Le produit scalaire vérifie les
propriétés suivantes :
 et
et
 des réels. Le produit scalaire vérifie les
propriétés suivantes :
des réels. Le produit scalaire vérifie les
propriétés suivantes :
Théorème [Théorème de Pythagore]
Si
et
sont deux vecteurs orthogonaux, on a
Théorème [Inégalité de Cauchy-Schwarz]
Si
et
sont deux vecteurs, on a
Il y a égalité si et seulement si
et
sont colinéaires.
Propriétés
Soient
et
deux vecteurs orthogonaux non nuls. Alors
forment une
base de
.
Géométrie du plan
→
II Géométrie du plan
→
II-4 Le plan euclidien
→ II-4-1 Propriétés du produit scalaire
II-4-2 Bases orthogonales
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Une base orthogonale de
est une base formée de deux vecteurs orthogonaux.
Elle est dite orthonormée si de plus ceux-ci sont unitaires (c'est-à-dire de norme 1).
La base est orthonormée.
Propriétés
Si
est une base orthonormée et si
,
,
alors
II-4-3 Version affine : la distance
Géométrie du plan
→
II Géométrie du plan
→
II-4 Le plan euclidien
→ II-4-3 Version affine : la distance
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Si
et
sont deux points du plan affine
, on appelle
distance
(euclidienne) de
à
le nombre
. On la note
.
Définition
Un repère affine orthonormé
est un repère affine tel que
est une
base orthonormée.
Exercice
Soient
,
,
. Trouver un repère affine orthonormé
tel que que
soit un vecteur directeur de la droite
et tel que
la deuxième coordonnée du point
dans ce repère soit positive ou nulle.
Exercice
Distances entre pions
Propriétés
Soit
un vecteur. L'ensemble des vecteurs orthogonaux à
est une
droite vectorielle d'équation
. On l'appelle la droite (vectorielle) orthogonale à
.
Définition
Si est d'équation , la droite vectorielle perpendiculaire à est d'équation .
Si et sont perpendiculaires et admettent respectivement comme équation et , alors .
Si a comme vecteur directeur , la droite vectorielle perpendiculaire à a comme vecteur directeur .
Propriétés
Deux droites perpendiculaires à une même droite sont parallèles. Si deux
droites sont parallèles, toute perpendiculaire à une est perpendiculaire à l'autre.
Géométrie du plan
→
II Géométrie du plan
→
II-4 Le plan euclidien
→ II-4-3 Version affine : la distance
II-4-4 Distance d'un point à une droite
Géométrie du plan
→
II Géométrie du plan
→
II-4 Le plan euclidien
→ II-4-4 Distance d'un point à une droite
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
Soient
une droite affine et
un point du plan. Il existe une unique droite
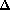 perpendiculaire à
et passant par
. Soient
un point de
et
un vecteur de base de la direction
de
. Le point d'intersection
de
et de
perpendiculaire à
et passant par
. Soient
un point de
et
un vecteur de base de la direction
de
. Le point d'intersection
de
et de
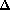 ,
appelé projeté orthogonal de
sur
vérifie :
,
appelé projeté orthogonal de
sur
vérifie :
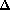 perpendiculaire à
et passant par
. Soient
un point de
et
un vecteur de base de la direction
de
. Le point d'intersection
de
et de
perpendiculaire à
et passant par
. Soient
un point de
et
un vecteur de base de la direction
de
. Le point d'intersection
de
et de
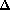 ,
appelé projeté orthogonal de
sur
vérifie :
,
appelé projeté orthogonal de
sur
vérifie :
Exercice
La distance de
à un point
de
est minimale pour le projeté orthogonal
de
sur
: pour tout point
de
, on a
Propriétés
La distance d'un point
à une droite
d'équation
est
On définit ainsi une application de dans qui à associe son projeté orthogonal sur . On l'appelle projection orthogonale sur .
Exercice
- Droite orthogonale
- Distance I
- Distance II
- Distance III
- Distance IV
- Projection I
- Projection II
Géométrie du plan
→
II Géométrie du plan
→
II-4 Le plan euclidien
→ II-4-4 Distance d'un point à une droite
II-4-5 Triangles
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Soit
un triangle non dégénéré. La hauteur issue du sommet
est la
perpendiculaire au côté opposé
passant par
. Le pied de cette hauteur est le projeté de
sur le
côté
.
Théorème [Pythagore]
Soit
un triangle rectangle en
, alors
De plus, si
est un triangle vérifiant l'égalité précédentes, il est rectangle en
.
Définition
La médiatrice de deux points distincts
et
est l'ensemble des points équidistants
de
et
. C'est la droite perpendiculaire à
passant par le milieu du segment
.
Propriétés
Les médiatrices d'un triangle non dégénéré sont concourantes.
Exercice
Comment calculer la distance de deux droites parallèles ? Utiliser plusieurs représentations
des droites (équation cartésienne, équations paramétriques).
Exercice
Soit
un triangle équilatéral de hauteur
. Soit
un point à l'intérieur du triangle.
Solution
- Montrer que la somme des distances de
aux côtés du triangle est égale à
.
- Soient , , les distances de à chacun des côtés , et respectivement. Montrer que est le barycentre de , ,
Solution
La somme des aires des trois triangles
,
et
est égale à l'aire du triangle
équilatéral qui est
si
est la longueur du côté.
D'autre part, l'aire de
est la moitié du produit de la distance de
à
par
. De même pour les autres triangles. Donc
la somme des distances est bien égale à
.
Ecrivons
comme barycentre de
,
,
avec
.
En mettant le côté
centré sur l'axe des
, on a
avec
porté par
et
perpendiculaire
à
.
Donc,
. De même pour les deux autres.
Exercice
Coordonnées trilinéaires
II-4-6 Cercles
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Le cercle de centre
et de rayon
est l'ensemble des points dont la distance
à
est
.
Définition
Le cercle circonscrit à un triangle non dégénéré est le cercle
passant par les sommets du triangle.
Propriétés
Propriétés
Une droite et un cercle sont soit sécants (si leur intersection est formée de deux
points distincts, soit tangents (un seul point d'intersection) soit disjoints.
Propriétés
Si
est un point du cercle
de centre
et de rayon
, il existe une unique tangente à
passant par
; elle a pour équation
C'est la perpendiculaire au rayon du cercle passant par
.
Théorème [droite d'Euler]
Le centre de gravité, l'orthocentre et le centre du cercle circonscrit
d'un triangle non dégénéré sont alignés.
II-4-7 Angles
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
On suppose connues la définition et propriété de base des
fonctions trigonométriques.
Par exemple,
Soient
et
deux vecteurs non nuls. On définit l'angle (orienté)
des vecteurs
et
comme le
nombre réel
modulo
tel que
Un vecteur unitaire s'écrit
où
est un nombre réel unique modulo
, c'est-à-dire unique à
l'addition près de
avec
un
entier relatif. On dit que
est un argument de
.
Théorème [Al-Kachi]
Si
est un triangle non dégénéré,
Propriétés
Soient
et
deux points distincts et
un angle non nul.
- L'ensemble des points du plan tels que l'angle soit égal à est un cercle passant par et privé de et .
- Soient un cercle
de centre
et
,
et
trois points du cercle. Alors,
III Isométries du plan
Géométrie du plan
→ III Isométries du plan
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Et maintenant passons aux isométries du plan : une isométrie conserve
les distances. Nous allons toutes les déterminer.
Définition
Une isométrie est une application de
dans
conservant les distances,
pour tous points
et
: autrement dit :
III-2 Le groupe des isométries
Géométrie du plan
→ III Isométries du plan
III-1 Des exemples
Géométrie du plan
→
III Isométries du plan
→ III-1 Des exemples
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Avant même de commencer, essayez de
deviner
de quelle isométrie il s'agit.
Géométrie du plan
→
III Isométries du plan
→ III-1 Des exemples
III-1-1 Les translations
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
On les a déjà
vu
. La translation de vecteur
associe
à tout point
du plan le point
tel que
. La composition
des deux translations de vecteur
et
est la translation de
vecteur
. Une translation transforme une droite en une droite
parallèle et conserve les angles.
En particulier,
En particulier,
III-1-2 Les rotations
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Soient un point du plan et un réel.
Définition
On appelle rotation de centre
et d'angle
l'application qui à un point
associe le point
tel que
et tel que l'angle orienté
est égal à
modulo
; l'image de
est
lui-même.
Exercice
On se donne deux points
et
et deux demi-droites
et
d'origine respective
et
de ces points.
Construire le centre de la rotation qui envoie
sur
. On pourra se donner
deux points
et
sur chacune des deux demi-droites
et
tels que
. Quelle est la condition sur les demi-droites pour que cette rotation
existe ?
Exercice
Construction du centre de rotation
Soir
une rotation de centre
et d'angle
.- Le point
est fixe et c'est le seul point fixe par
si l'angle de la rotation est non nul.
DémonstrationPar définition, donc . D'autre part, si est un autre point fixe,Donc l'angle de la rotation est nul.
-
est une isométrie et
.
DémonstrationOn desine et on regarde les triangles et . Les côtés et d'une part et et d'autre part sont égaux par définition de . On a alors l'égalité d'anglesDonc
Les deux triangles et ont deux côtés égaux et un angle égal, ils sont donc égaux. Donc les troisièmes côtés sont égaux :Ce qui prouve que est une isométrie. Les deux autres angles sont aussi égaux :
- la rotation respecte les angles et l'orientation
Démonstration
Propriétés
L'ensemble des rotations de centre
muni de la loi de composition des applications
est un groupe. Le composé d'une rotation et d'une translation est une rotation.
Démonstration
-
Le composé de deux rotations de centre
Le composé de deux rotations et de centre et d'angles respectifs et est une rotation de centre et d'angle : en effet,en prenant , on obtientPour les angles,
-
L'inverse d'une rotation
L'inverse de la rotation de centre et d'angle est la rotation de centre et d'angle .
-
Le composé d'une rotation et d'une translation
Étudions le composé d'une translation et d'une rotation . Construisons un point fixe géométriquement. Notons-le .
Le composé de deux isométries est une isométrie, donc on a bien la relationOn a d'autre part
Propriétés
Le composé de deux rotations est soit une rotation, soit une translation.
Ici les rotations n'ont pas forcément le même centre.Démonstration
Cherchons un point fixe.
On le note
.
La relation sur les angles se démontre ensuite toujours de la même manière
Exercice
Vérifier que
avec
Quel est le centre de rotation de , de ? Comment le construire géométriquement ?
Quel est le centre de rotation de , de ? Comment le construire géométriquement ?
Remarque
Dans le plan complexe, la rotation est donnée par
Prenons d'abord pour l'origine . Si et , on obtient
c'est-à-dire
On vérifie ainsi que la rotation de centre et d'angle est une application linéaire.
Pour quelconque, on a les formules
c'est-à-dire
avec
Le déterminant de la matrice est égal à .
Prenons d'abord pour l'origine . Si et , on obtient
On vérifie ainsi que la rotation de centre et d'angle est une application linéaire.
Pour quelconque, on a les formules
Le déterminant de la matrice est égal à .
III-1-3 Les réflexions
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Soit
une droite affine du plan
.
Définition
Le symétrique orthogonal d'un point
par rapport à
est le point
tel que la droite
soit perpendiculaire à
et tel que l'intersection de
et de
soit le milieu du segment
.
L'application
,
est appelée réflexion orthogonale
ou réflexion axiale ou symétrie orthogonale d'axe
.
Propriétés
Les points de la droite
sont invariants par la réflexion
. Les droites
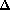 perpendiculaires à
sont globalement invariantes par
:
.
Une réflexion
transforme les angles en leur opposé :
perpendiculaires à
sont globalement invariantes par
:
.
Une réflexion
transforme les angles en leur opposé :
 perpendiculaires à
sont globalement invariantes par
:
.
Une réflexion
transforme les angles en leur opposé :
perpendiculaires à
sont globalement invariantes par
:
.
Une réflexion
transforme les angles en leur opposé :
Exercice
Construire l'axe de la réflexion donnée par les images d'un certain nombre
de points (à propos, combien de points sont-ils nécessaires pour déterminer
une réflexion) ?
Remarque
Prenons comme repère affine orthonormé
avec
un point de
,
un vecteur unitaire
sur
et
un vecteur unitaire normal à
. La réflexion
est donnée dans ce repère par
Soit l'angle que fait le vecteur avec le vecteur . On a donc , et on peut prendre . Alors la matrice de dans le repère est
Cela peut se voir géométriquement~. Si est l'image de par la réflexion , comme l'angle de porté par avec est , l'angle que fait avec son image est .
Le déterminant de est .
Soit l'angle que fait le vecteur avec le vecteur . On a donc , et on peut prendre . Alors la matrice de dans le repère est
Cela peut se voir géométriquement~. Si est l'image de par la réflexion , comme l'angle de porté par avec est , l'angle que fait avec son image est .
Le déterminant de est .
Exercice
La réflexion par rapport à une droite passant par
et
de vecteur normal
est donnée par
III-1-4 Les symétries glissées
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Que donne le composé d'une réflexion et d'une translation ?
Définition
Soit
une droite et
un vecteur parallèle à
.
On appelle symétrie glissée d'axe de glissage
et de vecteur
le composé de la réflexion
par la translation de vecteur
.
On a
Propriétés
Soit
un vecteur quelconque.
Soit
la réflexion par rapport à la droite
et
la translation de vecteur
.
- Si
est perpendiculaire à
,
est une réflexion par rapport à la droite translatée de
par le vecteur
- Si
n'est pas perpendiculaire à
, posons
avec
la projection de
sur
et
perpendiculaire à
et
soit
la droite translatée de
par le vecteur
.
Alors,
est la symétrie
glissée d'axe de glissage
et de vecteur
.
Exercice
Axe d'une symétrie glissée
Exemple
III-2 Le groupe des isométries
Géométrie du plan
→
III Isométries du plan
→ III-2 Le groupe des isométries
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Géométrie du plan
→
III Isométries du plan
→ III-2 Le groupe des isométries
III-2-1 Structure de groupe
Géométrie du plan
→
III Isométries du plan
→
III-2 Le groupe des isométries
→ III-2-1 Structure de groupe
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
L'ensemble des isométries de
forme un groupe que l'on note
.
En particulier :
- le produit (composé) de deux isométries est une isométrie ;
- une isométrie est une bijection de dans , elle admet une application réciproque qui est aussi une isométrie.
Rappel
La chose délicate à montrer est qu'une isométrie est bijective. Nous pourrons déduire ce fait de considérations d'algèbre linéaire. Mais nous allons ici le faire de manière géométrique.
Démonstration
Remarque
On a montré au passage les propositions suivantes :
Propriétés
Une isométrie qui laisse fixe trois points
non alignés est l'identité.
Propriétés
Toute isométrie peut être écrite comme le composé d'au plus
trois réflexions.
Géométrie du plan
→
III Isométries du plan
→
III-2 Le groupe des isométries
→ III-2-1 Structure de groupe
III-2-2 Les isométries positives
Géométrie du plan
→
III Isométries du plan
→
III-2 Le groupe des isométries
→ III-2-2 Les isométries positives
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
Une isométrie conservant l'orientation et ayant un point fixe est une rotation.
Démonstration
Le composé de deux rotations est une rotation ou une translation.
Démonstration
Démonstration
Soit
une isométrie laissant fixe un point
et conservant l'orientation. En particulier,
n'est
pas une réflexion. Supposons que
n'est pas l'identité.
Soit un point d'image distincte de et la rotation de centre envoyant sur . Alors laisse fixe et et préserve l'orientation.
Si n'est pas l'identité, prenons un point non fixe par . Comme et sont à égale distance de et de , la droite est la médiatrice de et . Donc coïncide avec la réflexion par rapport à la droite sur trois points, elle lui est donc égale. Comme conserve l'orientation, ce n'est pas possible. Donc, est l'identité et est une rotation.
Soit un point d'image distincte de et la rotation de centre envoyant sur . Alors laisse fixe et et préserve l'orientation.
Si n'est pas l'identité, prenons un point non fixe par . Comme et sont à égale distance de et de , la droite est la médiatrice de et . Donc coïncide avec la réflexion par rapport à la droite sur trois points, elle lui est donc égale. Comme conserve l'orientation, ce n'est pas possible. Donc, est l'identité et est une rotation.
Le composé de deux rotations est une rotation ou une translation.
Démonstration
Nous l'avons déjà vu, mais donnons-en une démonstration légèrement différente.
Soit
le composé de deux rotations. Nous avons montré par construction
que soit
a un point fixe, soit
est une translation. Si elle a un point fixe,
comme elle conserve l'orientation,
est une rotation.
Géométrie du plan
→
III Isométries du plan
→
III-2 Le groupe des isométries
→ III-2-2 Les isométries positives
III-2-3 Liste des isométries du plan
Géométrie du plan
→
III Isométries du plan
→
III-2 Le groupe des isométries
→ III-2-3 Liste des isométries du plan
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
Toute isométrie est d'un des types suivants :
- translation par un vecteur ;
- rotation d'angle de centre un point ;
- réflexion par rapport à une droite ;
- symétrie glissée obtenue en faisant une réflexion par rapport à une droite , puis en translatant par un vecteur non nul parallèle à .
Démonstration
On sait maintenant que toute isométrie est le composé
d'au plus trois réflexions. Qu'obtient-on pratiquement ? On suppose
dans la suite que
n'est pas l'identité.
- est une réflexion.
-
est le composé de deux réflexions par rapport à deux droites
et
.
Alors,
respecte l'orientation.
-
Les droites et sont parallèles
Alors est une translation.
-
les droites et ne sont pas parallèles
Le point d'intersection de et est fixe par : . Soit un point tel que est différent de . Soit la rotation de centre et envoyant sur . Alors a deux points fixes et .
Supposons que ne soit pas l'identité : soit un point différent de . Alors, est la médiatrice de . Soit la réflexion par rapport à la droite . Alors, est une isométrie laissant fixe trois points. C'est donc l'identité. Mais comme est une isométrie positive et une isométrie négative, ce n'est pas possible. Donc, est l'identité et est une rotation.
-
Les droites et sont parallèles
-
est le composé de trois réflexions
par rapport à trois droites
,
et
.
En particulier,
ne conserve pas l'orientation.
-
Les droites , et sont parallèles
L'isométrie est une translation de vecteur perpendiculaire à la direction des trois droites. Le composé avec est encore une réflexion par rapport à la droite translaté de
-
Les droites , sont parallèles
L'isométrie est une translation de vecteur perpendiculaire à la direction des deux droites et . Le composé avec est une réflexion glissée d'axe de glissage la droite translatée de par où est le projeté du vecteur sur une perpendiculaire à .
-
Les droites , sont parallèles
On traite ce cas comme le précédent.
-
Les droites , sont parallèles
Idem.
-
Les droites , et sont concourantes
Soit le point d'intersection de , et . Le composé est une rotation de centre que l'on peut écrire comme avec une droite convenable : plus précisément est la droite passant par dont l'angle avec est égal à l'angle de avec . On a alorsDonc, est une réflexion.
L'axe de symétrie passe par et est la droite des milieux . Pendre par exemple pour un point de .
-
Les droites , et ne sont pas concourantes
Le composé est une rotation de centre le point d'intersection de et et d'angle non nul. On peut l'écrire comme avec la droite parallèle à passant par et une droite convenable : plus précisément est la droite passant par dont l'angle avec est égal à l'angle de avec . On a alorsoù est un vecteur perpendiculaire à . Ce vecteur n'est pas perpendiculaire à car n'est pas parallèle à . Donc, est une réflexion glissée.
L'axe de glissage passe la projection de sur et par la projection de sur . En effet, l'image de par est son symétrique par rapport à la droite et l'axe de glissage passe par le milieu de . L'image par du symétrique de par rapport à est .
-
Les droites , et sont parallèles
Remarque
Le composé de trois réflexions est une réflexion si et
seulement si les droites sont parallèles ou concourantes. Sinon,
c'est une symétrie glissée de vecteur de translation non nul.
Géométrie du plan
→
III Isométries du plan
→
III-2 Le groupe des isométries
→ III-2-3 Liste des isométries du plan
III-2-4 Exercices
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Toute isométrie est le composé d'une isométrie ayant un point fixe et
d'une translation.
Exercice
Le composé de deux rotations de centres distincts est une isométrie positive. C'est donc soit
une translation, soit une rotation. Trouver géométriquement son centre ou le vecteur de translation.
Exercice
Composé de deux rotations
Exercice
Réflexion axiale et glissée
Exercice
Le composé d'une rotation non triviale et d'une translation est une isométrie positive. C'est
une rotation. Trouver géométriquement son centre.
Exercice
Composé d'une rotation et d'une translation
Exercice
Caractériser le composé d'une rotation et d'une réflexion.
Exercice
Composé d'une rotation et d'une réflexion
Exercice
Écrire une rotation comme composé de réflexions.
Exercice
Rotation : composé de réflexions
Exercice
Tracer l'axe du composé de trois réflexions.
Exercice
Produit de trois réflexions
III-3 Point de vue de l'algèbre linéaire
Géométrie du plan
→
III Isométries du plan
→ III-3 Point de vue de l'algèbre linéaire
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Géométrie du plan
→
III Isométries du plan
→ III-3 Point de vue de l'algèbre linéaire
III-3-1 Matrices orthogonales
Géométrie du plan
→
III Isométries du plan
→
III-3 Point de vue de l'algèbre linéaire
→ III-3-1 Matrices orthogonales
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Si est une matrice, la matrice transposée est par définition la matrice obtenue en échangeant les lignes et les colonnes :
Les matrices des rotations et des réflexions vérifient .
Définition
Propriétés
L'ensemble des matrices orthogonales forme un groupe pour le produit
des matrices. On le note
.
Propriétés
Les propriétés suivantes sont équivalentes :
- est orthogonale ;
- les colonnes de sont des vecteurs unitaires (deux à deux) orthogonaux ;
- l'application linéaire
de matrice
dans la base
vérifie
Propriétés
Le déterminant d'une application linéaire orthogonale est égal à
.
Propriétés
Les applications linéaires orthogonales de déterminant 1 sont les rotations
de
(laissant fixe
).
Géométrie du plan
→
III Isométries du plan
→
III-3 Point de vue de l'algèbre linéaire
→ III-3-1 Matrices orthogonales
III-3-2 Isométries
Géométrie du plan
→
III Isométries du plan
→
III-3 Point de vue de l'algèbre linéaire
→ III-3-2 Isométries
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
Soit
une application de
dans
. Alors, il y a équivalence
entre les propriétés suivantes :
- est une isométrie fixant l'origine ;
-
préserve le produit scalaire :
-
est la multiplication à gauche par une matrice orthogonale :
si
et
, alors
avec (application linéaire orthogonale).
Géométrie du plan
→
III Isométries du plan
→
III-3 Point de vue de l'algèbre linéaire
→ III-3-2 Isométries
III-4 Composé et transformé
Géométrie du plan
→
III Isométries du plan
→ III-4 Composé et transformé
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
On peut composer deux isométries mais il y a une opération plus naturelle : transformer une isométrie par une autre.
Définition
Soit
une isométrie. On appelle
- transformée par de la translation de vecteur la translation de vecteur .
- transformée par de la rotation de centre et d'angle la rotation de centre et d'angle ;
- transformée par de la réflexion orthogonale d'axe la réflexion orthogonale d'axe ;
On note la transformée de par . On parle aussi de conjuguée. Cette opération est beaucoup plus simple que la composée ! Il suffit de transformer les invariants.
Dans , on peut quand même interpréter la transformée comme un composé :
Propriétés
Le transformé de
par
est
.
Ainsi :
Si
est une figure, pour trouver le transformé de
par
, on commence par
prendre l'image réciproque de
par
(on déplace la figure).
Puis on applique par
, puis on transforme
par
(on la remet en place).- Soient
une translation de vecteur
et
la rotation de centre
et d'angle
.
Soit
l'image de
par
. Alors
autrement dit .
- Soient
la translation de vecteur
et
la réflexion par rapport à
. Soit
l'image de
par la translation
. Alors autrement dit, .
- On note
la réflexion orthogonale par rapport à la droite
,
la translation
de vecteur
,
la symétrie centrale par rapport à un point
du plan.
- si
est parallèle à
, autrement dit
- si
est perpendiculaire à
,
autrement dit
- autrement dit
- si
est parallèle à
,
On peut utiliser le fait que le carré d'une réflexion est l'identité pour simplifier les formules.
Géométrie du plan
→
III Isométries du plan
→ III-4 Composé et transformé
III-5 Formulaires
Géométrie du plan
→
III Isométries du plan
→ III-5 Formulaires
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
On note
la réflexion orthogonale par rapport à la droite
,
la translation
de vecteur
,
la symétrie centrale par rapport à un point
du plan.
Exercice
Démontrer les formules suivantes (et faire un dessin)
- ;
- si et sont deux droites parallèles, avec , et perpendiculaire aux deux droites ;
- Si
,
où
 est la droite perpendiculaire à
passant par
;
est la droite perpendiculaire à
passant par
;
- Si
,
où
 est la droite perpendiculaire à
passant par
,
et
la projection orthogonale de
sur
.
est la droite perpendiculaire à
passant par
,
et
la projection orthogonale de
sur
.
- Si
et
sont des droites affines passant par un point
et
l'angle
orienté de
et de
,
Exercice
Soit
un point de
et
une isométrie.
On peut écrire de manière unique
sous la forme
où
est une translation et où
est une isométrie laissant fixe le point
.
Vérifier que
.
Pratiquement :
Exercice
Décomposition d'une isométrie
- Si
est une translation, on prend pour
l'identité
et pour translation la translation
.
- Si
est une rotation de centre
, on prend pour
la rotation
de centre
et pour translation la translation de vecteur
.
Exemple
- Si
est une réflexion d'axe
, on prend la droite
parallèle à
et
passant par
,
la réflexion d'axe
et pour translation la
translation de vecteur
où
est le
vecteur perpendiculaire aux droites
et
avec
sur
.
Exemple
- Si
est une réflexion glissée d'axe
et de vecteur
(parallèle
à
),
on prend la droite
parallèle à
et
passant par
,
la réflexion d'axe
et pour translation la
translation de vecteur
où
est
le vecteur perpendiculaire aux droites
et
avec
sur
.
Géométrie du plan
→
III Isométries du plan
→ III-5 Formulaires
III-6 Exercices
Géométrie du plan
→
III Isométries du plan
→ III-6 Exercices
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Soit
la
réflexion d'axe la droite d'équation
. Pour chacune des translations
de vecteur
,
,
, soit
l'isométrie composée
.
Déterminer la nature de
et ses éléments caractéristiques.
Exercice
Soit
la rotation de centre
et d'angle
et
la
réflexion d'axe la droite d'équation
. Soit
l'isométrie composée
.
Montrer que
est une réflexion glissée. Préciser l'axe
et le vecteur de translation.
Exercice
- Soit
et
la rotation de centre
et
d'angle
. On écrit
comme le composé
d'une translation de vecteur
et d'une rotation de centre
.
Quel est l'angle de la rotation
? Calculer le vecteur
.
Faire de même en écrivant
.
- Faire de même avec la rotation de centre
et de d'angle
:
- Qu'obtient-on pour
?
- Écrire la rotation précédente comme composé de deux réflexions.
Géométrie du plan
→
III Isométries du plan
→ III-6 Exercices
IV Groupes et groupes d'isométrie
Géométrie du plan
→ IV Groupes et groupes d'isométrie
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Nous avons des groupes concrets à notre disposition, nous allons revenir aux groupes d'isométries du plan, autrement dit les groupes de symétrie d'un système. Dans ce paragraphe, nous n'étudierons de tels groupes que lorsqu'ils sont finis.
Les groupes que nous venons de rencontrer sont
- le groupe des isométries de laissant fixe (dans sa version vectorielle, le groupe des isométries de laissant fixe ) ;
- le groupe des rotations de laissant fixe , ou ce qui revient au même le groupe des isométries positives de laissant fixe ;
- le groupe des isométries ;
- le groupe des isométries positives de (rotation-translation) ;
- le groupe linéaire (le groupe des applications linéaires bijectives de ) ;
- le groupe affine des composés de translations et d'applications linéaires (laissant fixe ).
IV-1 Groupes d'isométries ou de symétrie
Nous n'avons pour l'instant donné que la définition d'un groupe. Il est temps d'en faire un peu plus :
Un groupe de symétrie qui est fini fixe toujours un point du plan et on peut complétement déterminer sa structure. C'est ce qu'on va faire dans le paragraphe suivant.
IV-7 Les groupes d'isométries du plan qui sont finis
Un groupe d'isométries qui n'est pas fini n'a pas toujours de points fixes : prenons par exemple le groupe des isométries d'une droite du plan. Pour l'étudier, on introduit la notion de groupe ponctuel (ou groupe vectoriel).
Géométrie du plan
→ IV Groupes et groupes d'isométrie
IV-1 Groupes d'isométries ou de symétrie
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-1 Groupes d'isométries ou de symétrie
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Soit
un ensemble de points dans le plan. L'ensemble des isométries
conservant
est un groupe et est appelé groupe de symétrie ou groupe d'isométries de
.
On le note ici
.
Remarque
Attention, un groupe de symétrie n'est pas formé que de symétries. Il n'est par contre formé
que d'isométries (en tout cas, dans notre contexte).
Exercice
Quel est le groupe de symétrie d'un point
? Quel est le lien entre le groupe
de symétrie de
et celui d'un autre point
?
Exercice
Quel est le groupe de symétrie de la droite de direction
(axe des
) ?
Quel est le groupe de symétrie de la droite d'équation
?
?
Si est fini, numérotons ses points ou même 1, ..., . Soit un élément de . On peut alors définir la permutation des points de
On a ainsi une action de sur l'ensemble .
Définition
Une action d'un groupe
sur un ensemble
est une application
qui vérifie les propriétés suivantes
- pour ;
- pour , , .
Exemple
Nous n'avons vu en fait ici que des groupes opérant sur un ensemble. Il s'agit
d'une notion très naturelle qu'on utilise sans le savoir:
-
opère sur
.
- Le groupe du carré opère sur l'ensemble
des sommets d'un carré.
- Le groupe du carré opère aussi sur l'ensemble des côtés du carré.
- Le groupe du carré opère sur l'ensemble des couples formés d'un côté et d'un de ses sommets. Combien d'éléments l'ensemble a-t-il ?
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-1 Groupes d'isométries ou de symétrie
IV-2 Sous-groupes et ordre
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-2 Sous-groupes et ordre
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Soit
un groupe muni d'une loi
. Un sous-groupe est un sous-ensemble
de
tel que
- si et appartiennent à , appartient à ;
- l'élément neutre de appartient à ;
- si appartient à , appartient à .
Exercice
- L'ensemble des matrices de la forme avec est un sous-groupe de .
- L'ensemble des matrices de la forme avec et est un sous-groupe de .
Définition
L'ordre d'un élément
d'un groupe
est le plus petit entier
strictement positif tel que
s'il existe et
 sinon.
sinon.
 sinon.
sinon.
Exercice
- Soient et deux réflexions d'axe et . Quel est l'ordre de et ? de leur composé ?
- Soit
une rotation d'angle
et
une translation. Calculer l'ordre
de
.
- Calculer l'ordre de , de , de .
Propriétés
L'ordre d'un élément d'un groupe fini divise l'ordre du groupe.
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-2 Sous-groupes et ordre
IV-3 Sous-groupe engendré
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-3 Sous-groupe engendré
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Soit
un sous-ensemble d'un groupe
.
Le sous-groupe de
engendré par
est le plus petit sous-groupe de
contenant
. On dit aussi que
est engendré par
.
Exercice
Quel est le sous-groupe de
engendré par toutes
les réflexions de
? par les symétries centrales ?
Exercice
Si
est un triangle équilatéral de centre de gravité
,
quel est le sous-groupe
de
engendré par la rotation d'angle
de centre
? Par deux de ses réflexions ?
Exercice
Si
est un rectangle,
donner un ensemble de générateurs de
(le moins possible). Faire de même pour
un carré.
Exercice
Étudier le sous-groupe de
engendré par les matrices
,
.
Combien a-t-il d'éléments ? Quel ordre ont-ils ? Donner la table de multiplication.
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-3 Sous-groupe engendré
IV-4 Groupe cyclique
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-4 Groupe cyclique
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Exemple
Le groupe
engendré par la rotation
de centre
et d'angle
est un groupe d'ordre
.
Compléter la table de groupe pour
, pour
:
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-4 Groupe cyclique
IV-5 Morphismes de groupes
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-5 Morphismes de groupes
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Un homomorphisme de groupes d'un groupe
dans un groupe
(notés tous deux multiplicativement)
est une application
de
dans
telle que
pour tous
,
dans
.
Un isomorphisme de groupes est un homomorphisme de groupes qui est bijectif. On dit alors que les groupes et sont isomorphes.
Un isomorphisme de groupes est un homomorphisme de groupes qui est bijectif. On dit alors que les groupes et sont isomorphes.
Exercice
Soient
et
deux points de
. Soient
et
les groupes de symétrie laissant fixe
et
respectivement.
Déterminer explicitement un isomorphisme de
sur
.
Exemple
Si
agit sur un ensemble
, l'application
qui à
associe la bijection de
:
est un homomorphisme de groupes.
Exercice
Nombre d'isométries
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-5 Morphismes de groupes
IV-6 Sous-groupes invariants
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-6 Sous-groupes invariants
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Définition
Un sous-groupe normal ou sous-groupe distingué
ou sous-groupe invariant
d'un groupe
est un sous-groupe de
tel que
pour tout
.
Exemple
- Le sous-groupe des rotations est un sous-groupe distingué du groupe , puisque le transformé d'une rotation de centre par une isométrie laissant fixe est encore une rotation de centre .
- Par contre le transformé d'une rotation de centre par une translation par un vecteur non nul n'est pas une rotation de centre . Donc n'est pas distingué dans .
Exercice
Pour les groupes
,
,
,
,
,
, écrire les relations d'inclusion
qui existent entre eux et pour chacune d'entre elles, dire
si le plus petit est un sous-groupe distingué du plus gros.
Exercice
Soit
une figure (un ensemble de points).
Alors
. Soit
un sous-groupe de symétrie
contenant
. Alors,
est distingué dans
si et seulement si
et
ont
même groupe de symétrie pour tout
.
Trouver le sous-groupe de symétrie de figures
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-6 Sous-groupes invariants
IV-7 Les groupes d'isométries du plan qui sont finis
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-7 Les groupes d'isométries du plan qui sont finis
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Propriétés
Soit
un groupe fini du groupe des isométries de
. Il existe un point
de
qui est fixe par tous les éléments de
:
Démonstration
- On prend un point
dans le plan et on construit les images de
par
tous les éléments de
. Comme
est fini formé de
isométries
, ...,
,
on obtient ainsi
points
Soit l'isobarycentre de , ..., .
- Appliquons à
n'importe
lequel des éléments
de
. Alors, l'ensemble des
est l'ensemble
des éléments de
qui se trouvent sur la ligne correspondant à
dans le tableau de la
loi,
c'est donc en fait exactement tous les
mais dans un ordre différent.
Donc l'isobarycentre des
est l'isobarycentre des
c'est-à-dire
.
-
Il reste à voir que l'image par
de
est aussi l'isobarycentre des
.
Toute isométrie est le composé d'une translation et d'une isométrie
laissant fixe un point. On vérifie que cela est vrai pour deux telles isométries et
donc pour leur composé.
- Donc .
Théorème
Soit
un sous-groupe fini du groupe des isométries laissant fixe un point
. Alors,
est l'un des groupes suivants pour un entier
- le sous-groupe de
engendré par la rotation de centre
et d'angle
;
- le sous-groupe de engendré par la rotation de centre et d'angle et une réflexion axiale d'axe passant par .
Corollaire
Si le groupe de symétrie
d'une figure est fini, il existe un point du plan
et un entier
tel que
soit
Ainsi, si le groupe de symétrie d'une figure est fini et
s'il contient une réflexion, c'est un groupe diédral.- soit le sous-groupe de engendré par la rotation de centre et d'angle ,
- soit le sous-groupe de engendré par la rotation de centre et d'angle et une réflexion axiale d'axe passant par (on l'appelle groupe diédral).
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-7 Les groupes d'isométries du plan qui sont finis
IV-8 Exercices
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-8 Exercices
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Le groupe du deuxième type (groupe diédral
)
est un groupe d'ordre
. Construire sa table de groupe pour
.
Exercice
De quel type est le groupe du triangle ? du rectangle ? du losange ?
d'un pentagone régulier ?
Exercice
Calcul dans le groupe diédral
Trouver le groupe de symétrie de figures
Exercice
Dessiner un ensemble
dont le groupe d'isométries
est formé exactement des rotations d'angle un multiple entier de
et de centre
un point
.
Exercice
Dessiner un ensemble
dont le groupe d'isométries positives
est formé exactement des rotations d'angle un multiple entier de
de centre
et dont le groupe des isométries contient une symétrie axiale passant par
.
Quel est le nombre d'éléments du groupe d'isométries de
?
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-8 Exercices
IV-9 Coloriages
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-9 Coloriages
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Nous allons ici montrer quelques coloriages d'un polygone
régulier à
côtés
compatibles (en un sens
à définir) avec son groupe de symétrie.
IV-9-3 Stabilisateur d'une couleur
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-9 Coloriages
IV-9-1 Que colorier
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
On peut imaginer de colorier ses sommets ou ses côtés. Mais artistiquement, ce n'est pas très
satisfaisant. Aussi allons-nous d'abord associer à un sommet ou à un côté un petit triangle
ou quadrilatère
dont un des sommets est au centre de gravité du polygone.
On trouve triangles. Le groupe de symétrie de est d'ordre . Le stabilisateur d'un sommet, c'est-à-dire le sous-groupe des isométries qui stabilisent (laissent fixe) ce sommet, est formé de l'identité et de la symétrie par rapport à la droite passant par ce sommet et par le centre de .
On peut aussi vouloir colorier les couples formés d'un sommet et d'un côté qui le contient. On obtient alors triangles.
On dit que agit transitivement sur l'ensemble des sommets (ou l'ensemble des côtés).
On trouve triangles. Le groupe de symétrie de est d'ordre . Le stabilisateur d'un sommet, c'est-à-dire le sous-groupe des isométries qui stabilisent (laissent fixe) ce sommet, est formé de l'identité et de la symétrie par rapport à la droite passant par ce sommet et par le centre de .
On peut aussi vouloir colorier les couples formés d'un sommet et d'un côté qui le contient. On obtient alors triangles.
Exercice
Prenons un couple
de sommets ou de côtés.
Montrer qu'il existe une isométrie de
qui
envoie
sur
.
On dit que agit transitivement sur l'ensemble des sommets (ou l'ensemble des côtés).
IV-9-2 Comment colorier
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Nous allons colorier ces triangles de manière régulière, ce qui signifie que ce
coloriage doit être compatible avec la définition abstraite suivante :
Voici des exemples de bons coloriages (compatibles au groupe d'isométries du polygone).
et voici des exemples de mauvais coloriages
Définition
Soit
un groupe opérant transitivement sur un ensemble
, (si
et
sont dans
,
est l'image de
par un élément de
).
Un coloriage de
compatible avec
est une famille de sous-ensembles
de
:
- formant une partition : la réunion des est et les ensembles sont disjoints deux à deux : ;
- tel que pour tout et pour tout , est un des de la famille.
Voici des exemples de bons coloriages (compatibles au groupe d'isométries du polygone).
IV-9-3 Stabilisateur d'une couleur
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→
IV-9 Coloriages
→ IV-9-3 Stabilisateur d'une couleur
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Si
est dans
, on note
la "couleur" de
, c'est-à-dire l'ensemble
auquel appartient
.
On peut associer à ce coloriage un sous-groupe de
: le stabilisateur d'une couleur,
c'est-à-dire, si on prend comme couleur
, l'ensemble des
tel que
. On le note
.
On a la propriété suivante
Démonstration
En particulier, si , c'est-à-dire si est dans le stabilisateur de , est dans le stabilisateur de la couleur de :
Choisissons une couleur et soit son stabilisateur. Les autres couleurs sont de la forme pour un certain et le stabilisateur de est
On a la propriété suivante
Propriétés
Soient
et
. Si
appartient à
, alors
appartient à
.
Démonstration
Puisque
et
appartiennent à
, l'intersection
est non vide. Donc par définition d'un coloriage,
et
est donc dans le
stabilisateur de
.
En particulier, si , c'est-à-dire si est dans le stabilisateur de , est dans le stabilisateur de la couleur de :
Choisissons une couleur et soit son stabilisateur. Les autres couleurs sont de la forme pour un certain et le stabilisateur de est
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→
IV-9 Coloriages
→ IV-9-3 Stabilisateur d'une couleur
IV-9-4 Comment construire les coloriages
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→
IV-9 Coloriages
→ IV-9-4 Comment construire les coloriages
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Nous allons donner une méthode de construction de coloriages de pour l'ensemble des sommets, ou des côtés, ou des couples sommets/côtés, en partant d'un sous-groupe de .
- Choisissons un élément
de
et un sous-groupe
de
. D'après ce qu'on vient d'étudier, pour que
puisse être le stabilisateur de la couleur
de
, il est nécessaire que
contienne le stabilisateur de
(qui est le sous-groupe engendré par une réflexion dans le cas des sommets ou des côtés et le groupe trivial
dans le cas des sommets/côtés). On le suppose donc.
-
Soit
. Vérifions que les
pour
vérifient la propriété
des coloriages. Notons les ensembles distincts
pour
.
Comme
agit transitivement sur
, la réunion des
est tout
. Il reste à montrer que si
est non vide, alors
.
Soit
un élément de
,
on a donc en écrivant tout ce qu'on sait,
avec et appartenant à . D'oùce qui implique que appartient au stabilisateur de , donc à . Donc, et
- Ainsi, les sous-ensembles pour forment bien un coloriage de .
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→
IV-9 Coloriages
→ IV-9-4 Comment construire les coloriages
IV-9-5 Exercices
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Exercice
Trouver tous les coloriages obtenus ainsi pour un carré, un hexagone, un nonagone.
Dans chacun des cas, regarder si le stabilisateur d'une couleur est indépendant de
la couleur ou non. Dans le premier cas, quelle propriété de ce sous-groupe en découle-t-il ?
Exercice
Coloriages de polygones
Exercice
Pour récapituler :
- On considère un polygone régulier à 9 côtés. Décrire son groupe de symétrie (nom, nombre d'éléments, générateurs, ...)
- On trace les triangles dont un sommet est au centre du polygone et tel que le côté opposé à ce sommet soit un demi-côté (allant d'un sommet au milieu des côtés dont il est l'extrémité). Combien y a-t-il de tels triangles ?
- Soit une rotation d'angle et le sous-groupe qu'il engendre dans . Dessiner un coloriage de ces triangles construit associé à . Combien de couleurs faut-il ? Dessiner tous les coloriages à deux ou trois couleurs compatibles avec et donner le stabilisateur d'une des couleurs dans chaque cas.
IV-10 Groupe ponctuel
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-10 Groupe ponctuel
- I De la géométrie aux groupes
- II Géométrie du plan
- III Isométries du plan
- IV Groupes et groupes d'isométrie
- Index
Soit
un point de
,
et
deux isométries. Écrivons-les
comme
et
avec
et
des vecteurs,
et
des isométries laissant fixe
.
Cette écriture est unique.
Attention, il n'y a aucune raison que soit contenu dans . Un premier exemple de cette situation est le suivant : soit le groupe engendré par la rotation de centre et d'angle ; est engendré par la rotation de centre et d'angle . Mais cet exemple est un peu artificiel ...
Si l'on peut, on choisit l'origine de manière à simplifier les calculs. Modulo conjugaison, le groupe ponctuel qu'on note abusivement n'en dépend pas.
Par exemple, si est une figure dont le groupe d'isométrie est fini, le meilleur choix pour calculer son groupe ponctuel est bien sûr le centre de gravité de . Avec ce choix, .
Groupe ponctuel d'une frise
Propriétés
- Comportement par composition : pour un vecteur .
- Soit un groupe d'isométries et soit l'ensemble des isométries laissant fixe obtenues de la manière précédente à partir des éléments de . Alors, est un groupe.
- Si
est un autre point de
et si
la translation de vecteur
(ainsi,
), on a
Exercice
Soit
un rectangle. Soit
son groupe de symétrie.
Si
est le point d'intersection de ses diagonales, que vaut
? Si
est un point qui n'est pas le point d'intersection de ses diagonales, que vaut
? Quel est son ordre ?
Attention, il n'y a aucune raison que soit contenu dans . Un premier exemple de cette situation est le suivant : soit le groupe engendré par la rotation de centre et d'angle ; est engendré par la rotation de centre et d'angle . Mais cet exemple est un peu artificiel ...
Définition
Soit
un groupe d'isométries et
un point du plan.
Le groupe de symétrie ponctuel ou groupe de symétrie vectoriel
est par définition l'ensemble des isométries
pour
.
Si l'on peut, on choisit l'origine de manière à simplifier les calculs. Modulo conjugaison, le groupe ponctuel qu'on note abusivement n'en dépend pas.
Par exemple, si est une figure dont le groupe d'isométrie est fini, le meilleur choix pour calculer son groupe ponctuel est bien sûr le centre de gravité de . Avec ce choix, .
Exercice
Groupe ponctuel d'une frise
Géométrie du plan
→
IV Groupes et groupes d'isométrie
→ IV-10 Groupe ponctuel