Intégration numérique
Intégration numérique
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Ce document présente quelques méthodes classiques de calcul numérique d'intégrales. Il est destiné à des étudiants de licence.
II Formules de quadrature et leur ordre
IV Etude de l'erreur d'une méthode de quadrature
V Exemples de calcul numérique de l'ordre
Vous trouverez ici le fichier pdf de ce document docintegnum.pdf
I Introduction
Intégration numérique
→ I Introduction
I-1 Problème étudié
Intégration numérique
→
I Introduction
→ I-1 Problème étudié
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Soit une fonction
intégrable. Nous nous
intéressons au calcul de son intégrale sur
:
Dans ce chapitre on présente la théorie des quelques
méthodes classiques de calcul numérique de
. Ces méthodes sont appelées
méthodes de quadrature . Pour chaque méthode, on s'intéresse à son ordre,
à l'étude de sa convergence et à l'étude de son erreur de convergence.
On développe aussi quelques idées nécessaires à l'écriture d'un
programme numérique pour le calcul de
.
I-2 Notations et définitions
Intégration numérique
→
I Introduction
→ I-2 Notations et définitions
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Soit
bornée et soit
une subdivision de
de pas
On pose:
Définition [Intégrale de Riemann]
La fonction
est dite Riemann intégrable si
. Dans ce
cas, on note
le réel
et on l'appelle l'intégrale de Riemann
associée à
.
Remarque
- Toute fonction continue par morceaux est Riemann intégrable.
- Toute fonction monotone est Riemann intégrable.
I-3 Résultats fondamentaux
Intégration numérique
→
I Introduction
→ I-3 Résultats fondamentaux
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Proposition
Si
est Riemann intégrable, alors
ou d'une manière équivalente
Remarque
Si
est continue alors
Théorème
Si
est continue alors
et d'une façon plus générale
II Formules de quadrature et leur ordre
Intégration numérique
→ II Formules de quadrature et leur ordre
II-1 Idée de base
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-1 Idée de base
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
La plupart des algorithmes numériques procèdent comme suit : on
subdivise l'intervalle
en plusieurs sous-intervalles
et on utilise le fait que
De cette manière, on est amené au calcul de plusieurs
intégrales pour lesquelles la longueur de l'intervalle d'intégration
est relativement petite. Prenons une de ces intégrales, notons
la longueur de l'intervalle et
. Un changement de variable
nous donne alors:
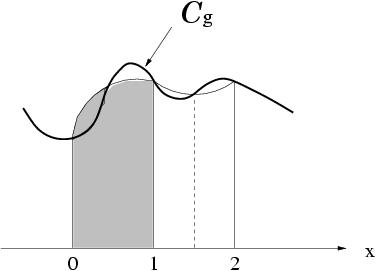
Il reste alors à calculer une approximation de

Il reste alors à calculer une approximation de
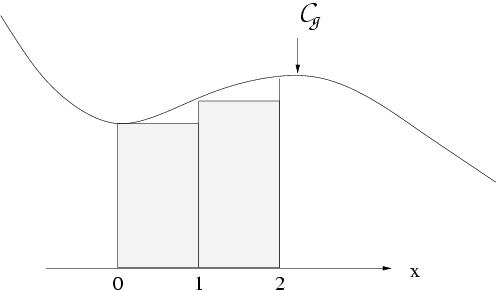
II-2 Méthode des rectangles à gauche
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-2 Méthode des rectangles à gauche
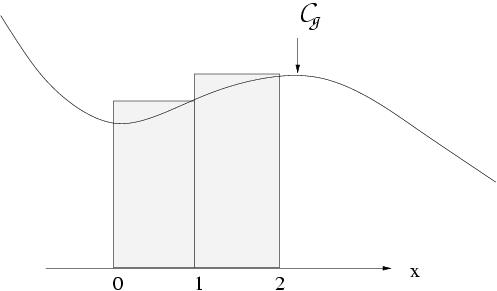
II-3 Méthode des rectangles à droite
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-3 Méthode des rectangles à droite
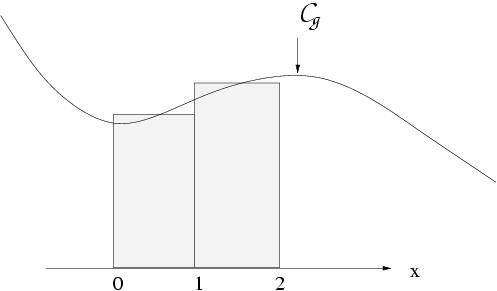
II-4 Méthode du point milieu
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-4 Méthode du point milieu
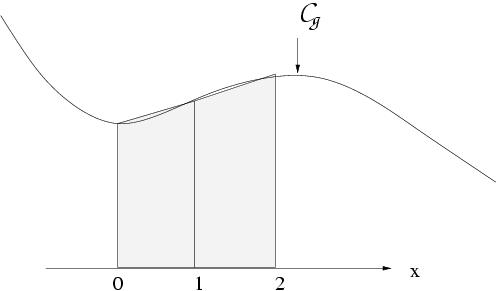
II-5 Méthode du trapèze
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-5 Méthode du trapèze
II-6 Méthode de Simpson
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-6 Méthode de Simpson
II-7 Méthode de Newton-Cotes
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-7 Méthode de Newton-Cotes
II-8 Ordre
Intégration numérique
→
II Formules de quadrature et leur ordre
→ II-8 Ordre
II-8-1 Définition
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Définition
On dit que l'ordre ordre d'une formule de quadrature de la formule de
quadrature
est
si
elle est exacte pour tous les polynômes de degré inférieur
ou égal à
, c'est-à-dire: pour
polynôme de degré
,
On voit que les formules du point milieu et des trapèzes sont d'ordre 2. La formule de Newton-Cotes à étages a un ordre supérieur ou égal à .
Le tableau suivant résume l'ordre ainsi que les poids des différentes méthodes de quadrature pour
Tableau
s | ordre | nom | |||||||
| 1 | 1 | 1 | rectangle | ||||||
1 | 2 | 1 | pt. milieu | ||||||
2 | 2 | trapèze | |||||||
3 | 4 | Simpson | |||||||
4 | 4 | Newton | |||||||
5 | 6 | Boole | |||||||
6 | 6 | Boole | |||||||
7 | 8 | Weddle |
Exercice
Ordre d'une méthode de quadrature
II-8-2 Condition nécessaire et suffisante
Intégration numérique
→
II Formules de quadrature et leur ordre
→
II-8 Ordre
→ II-8-2 Condition nécessaire et suffisante
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Théorème
La formule de
quadrature
est d'ordre
si et seulement
si:
Preuve
La nécessité de
l'équivalence
) est une conséquence de
la
formule
)
si l'on pose
. Pour en montrer la suffisance, on
utilise le fait qu'un polynôme de degré
est une combinaison
linéaire de
et que l'intégrale
ainsi que l'expression
sont linéaires en
.
II-8-3 Remarque sur l'ordre
Intégration numérique
→
II Formules de quadrature et leur ordre
→
II-8 Ordre
→ II-8-3 Remarque sur l'ordre
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Remarque
- En fixant les noeuds
(distincts), la
condition
avec
représente un système linéaire pour
Comme la matrice dans la formule est inversible (matrice de Vandermonde), la résolution de ce système nous donne une formule de quadrature d'ordre .
- Si l'on vérifie les
conditions
pour la formule de
Simpson, on fait une observation intéressante: par définition, il
est évident que la
condition
est satisfaite pour
,
,
, mais on remarque qu'elle est aussi satisfaite pour
. En effet:
Elle est donc d'ordre 4. Par conséquent, elle n'est pas seulement exacte pour les polynômes de degré 2 mais aussi pour les polynômes de degré 3. Ceci est est une propriété qui peut être généralisée aux formules de quadrature symétriques (c'est-à-dire ).
Coefficients et noeuds d'une formule de quadrature symétrique
II-8-4 Cas symétrique
Intégration numérique
→
II Formules de quadrature et leur ordre
→
II-8 Ordre
→ II-8-4 Cas symétrique
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Théorème
Une formule de quadrature symétrique a toujours un ordre
pair: si elle est exacte pour les polynômes de
degré
, elle est exacte pour les polynômes de
degré
.
Preuve
Chaque polynôme
de degré
peut être
écrit sous la forme
où
est un polynôme de degré
et où
est
une constante. Il suffit alors de montrer que la formule symétrique
est exacte pour
. A cause de la
symétrie de cette fonction, la valeur exacte vaut
Pour une formule de quadrature symétrique on a
Donc l'approximation numérique de est également nulle.

Donc l'approximation numérique de est également nulle.
III Mise en oeuvre sur Matlab
Intégration numérique
→ III Mise en oeuvre sur Matlab
III-1 Notations
Intégration numérique
→
III Mise en oeuvre sur Matlab
→ III-1 Notations
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Ici nous allons exécuter sur Matlab quelques méthodes de quadrature classiques pour
approcher la valeur de l'intégrale
avec une subdivision de l'intervalle
correspondante à
III-2 Méthode des rectangles à gauche
Intégration numérique
→
III Mise en oeuvre sur Matlab
→ III-2 Méthode des rectangles à gauche
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On note
l'approximation de
par la méthode des
rectangles à gauche et
l'erreur commise. Voici un programme
Matlab qui calcule
et
:
Code Matlab
Les résultats obtenus par ce programme sont:
Code Matlab
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
Iexa = log(2);
alpha = 1;
beta = 2;
N = 4;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Irg = 0.0;
for i = 1:N
Irg = Irg + h*f(x(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Irg
Erg = abs(Iexa - Irg)
%%%%%%%%%%%%%%%%%%%%%%%%
Les résultats obtenus par ce programme sont:
Irg = 7.595238095e-01 Erg = 6.637662896e-02
III-3 Méthode des trapèzes
Intégration numérique
→
III Mise en oeuvre sur Matlab
→ III-3 Méthode des trapèzes
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On note
l'approximation de
par la méthode des
trapèzes et
l'erreur commise. Voici un programme
Matlab qui calcule
et
:
Code Matlab
Les résultats obtenus par ce programme sont:
Code Matlab
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
Iexa = log(2);
alpha = 1;
beta = 2;
N = 4;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Itr = 0.0;
for i = 1:N
Itr = Itr + h*(0.5*f(x(i)) + 0.5*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Itr
Etr = abs(Iexa - Itr)
Les résultats obtenus par ce programme sont:
Itr = 6.970238095e-01 Etr = 3.876628964e-03
III-4 Méthode de Simpson
Intégration numérique
→
III Mise en oeuvre sur Matlab
→ III-4 Méthode de Simpson
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On note
l'approximation de
par la méthode de
Simpson et
l'erreur commise. Voici un programme
Matlab qui calcule
et
:
Code Matlab
Les résultats obtenus par ce programme sont:
Code Matlab
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
Iexa = log(2);
alpha = 1;
beta = 2;
N = 4;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Isi = 0.0;
for i = 1:N
Isi = Isi+h*(1/6*f(x(i))+2/3*f((x(i)+x(i+1))/2)+1/6*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Isi
Es = abs(Iexa - Isi)
Les résultats obtenus par ce programme sont:
Isi = 6.931545307e-01 Esi = 7.350094585e-06
III-5 Commentaires des résultats
Intégration numérique
→
III Mise en oeuvre sur Matlab
→ III-5 Commentaires des résultats
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On voit bien que l'erreur absolue obtenue par la méthode de Simpson
est beaucoup plus faible que celles obtenues par les deux autres. Ceci
confirme la règle: plus l'ordre de la méthode est grand, plus la
précision est bonne .
IV Etude de l'erreur d'une méthode de quadrature
Intégration numérique
→ IV Etude de l'erreur d'une méthode de quadrature
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Pour étudier l'erreur commise en approchant une intégrale par
l'une des formules de quadrature, nous commençons par une
expérience numérique :
IV-1 Expérience numérique
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→ IV-1 Expérience numérique
IV-1-1 Nombre d'évaluation
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→
IV-1 Expérience numérique
→ IV-1-1 Nombre d'évaluation
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Prenons une fonction
définie sur
, subdivisons l'intervalle en plusieurs
sous-intervalles équidistants (
) et
appliquons l'une des formules de quadrature du paragraphe
précédent. Ensuite, étudions l'erreur (en échelle
logarithmique),
en fonction du nombre d'évaluations
de la fonction
pour Newton-Cotes :
est défini par:
Le nombre
repésente une mesure pour le travail effectué par l'ordinateur.
IV-1-2 Exemple
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Voici les résultats obtenus par les formules de
Newton-Cotes (trapèzes, Simpson, Boole) pour l'int'grale
et
Code Matlab
La figure ci-dessous montre donne les résultats pour
Code Matlab
clear all;
Iexa = sin(2);
alpha = 0;
beta = 2;
f = inline('cos(x)','x');
%--------------------------
%--------------------------
% Méthode des trapèzes
%--------------------------
%--------------------------
s = 2;
for j = 1:1:10
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
fetr(j) = log10(N*(s-1) +1);
h = (beta - alpha)/N;
x = [alpha:h:beta];
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Itr=0.0;
for i = 1:N
Itr = Itr + h*(1/2*f(x(i)) + 1/2*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Etr(j) = log10(abs(Iexa - Itr)) ;
end
%--------------------------
%--------------------------
% Méthode de Simpson
%--------------------------
%--------------------------
s = 3;
for j=1:1:10
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
fesi(j) = log10(N*(s-1) +1);
h = (beta - alpha)/N;
x = [alpha:h:beta];
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Isi = 0.0;
for i = 1:N
Isi = Isi+h*(1/6*f(x(i))+2/3*f((x(i)+x(i+1))/2)+1/6*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Esi(j) = log10(abs(Iexa - Isi)) ;
end
%--------------------------
%--------------------------
% Méthode de Boole (s=6)
%--------------------------
%--------------------------
s = 6;
for j = 1:1:8
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
febo(j) = log10(N*(s-1) +1);
h = (beta - alpha)/N;
x = [alpha:h:beta];
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Ibo = 0.0;
for i = 1:N
Ibo = Ibo + h*(19/288*f(x(i)) + 75/288*f(x(i)+h/5) +
50/288*f(x(i)+(2*h/5)) + 50/288*f(x(i)+ (3*h/5)) +
75/288*f(x(i)+ (4*h/5)) + 19/288*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Ebo(j) = log10(abs(Iexa - Ibo)) ;
plot(fetr, Etr, 'k-.', fesi, Esi, 'k-+', febo, Ebo, 'k-*')
legend('Trapèzes', 'Simpson', 'Boole (s=6)')
xlabel('log10(Erreur)');
ylabel('log10(fe)');
title('Le travail fe en fonction de l''erreur');
end
La figure ci-dessous montre donne les résultats pour

IV-1-3 Interprétation des résultats
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→
IV-1 Expérience numérique
→ IV-1-3 Interprétation des résultats
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Nous constatons que:
- dépend linéairement du nombre de chiffres exacts, donné par .
- La pente de chaque droite est où est l'ordre de la méthode de quadrature.
- Pour un travail équivalent (même ), les formules avec un ordre élevé ont une meilleure précision.
IV-1-4 Justification des résultats
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→
IV-1 Expérience numérique
→ IV-1-4 Justification des résultats
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Etudions d'abord l'erreur faite sur un sous-intervalle de longueur
.
On considère la formule de quadrature d'ordre . En supposant que est suffisament différentiable, on peut remplacer et par les séries de Taylor au voisinage de :
La constante définie par
s'appelle constante de l'erreur. Si on suppose que est assez petit pour négliger devant , on obtient:
Cette formule nous permet de mieux comprendre les
résultats de la figure précédente. En effet, on peut écrire
et
. Par conséquent,
Ceci montre la dépendance linéaire entre
et
et le fait que la pente
soit de
.
On considère la formule de quadrature d'ordre . En supposant que est suffisament différentiable, on peut remplacer et par les séries de Taylor au voisinage de :
s'appelle constante de l'erreur. Si on suppose que est assez petit pour négliger devant , on obtient:
IV-2 Estimation rigoureuse de l'erreur
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→ IV-2 Estimation rigoureuse de l'erreur
IV-2-1 Noyau de Peano
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→
IV-2 Estimation rigoureuse de l'erreur
→ IV-2-1 Noyau de Peano
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Dans ce paragraphe on s'occupe de l'estimation
exacte de l'erreur d'une formule de quadrature en vue de démontrer
les théorèmes de convergence et assurer une certaine précision
du résultat numérique.
Preuve
Exemple
Théorème [et Définition]
Soit une formule de quadrature d'ordre
et un entier
vérifiant
. Considérons une fonction
de classe
, alors l'erreur
définie par la
formule
vérifie:
où
est le noyau de Peano , défini par:
Preuve
La formule de Taylor avec reste intégral appliquée à
au point
donne:
En combinant cette dernière formule avec la
formule
et en utilisant
le fait que
et en remarquant que la partie polynomiale dans l'avant-dernière équation ne
contribue pas à l'erreur (à cause que
), nous obtenons:
Une évaluation de l'intégrale intérieure donne le résultat.
Remarque
Pour une formule de quadrature d'ordre
et un entier
vérifiant
on a:
où
est la constante de l'erreur
définie par la
formule
.
Exemple
Les noyaux de Peano pour la méthode du point milieu sont donnés
par:
IV-2-2 Majoration de l'erreur
Intégration numérique
→
IV Etude de l'erreur d'une méthode de quadrature
→
IV-2 Estimation rigoureuse de l'erreur
→ IV-2-2 Majoration de l'erreur
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Nous sommes maintenant en mesure d'estimer l'erreur commise pour
l'intervalle
tout entier et ceci pour une subdivision
arbitraire
. Rappelons que, comme dans la
formule
,
l'erreur est donnée par:
On a alors le théorème suivant:
Preuve
Exemple
Exercice
Théorème
Soit une formule de quadrature d'ordre
et un entier
vérifiant
. Considérons une fonction
de classe
. Alors l'erreur
définie par
la
formule
vérifie
l'estimation suivante:
où .
où .
Preuve
La
formule
donne:
Comme
l'erreur
est la somme des erreurs sur les
sous-intervalles de la subdivision, nous obtenons:
et puisque
, on obtient
l'équation
.
Exemple
Pour la formule du point milieu, on a:
Pour la formule des trapèzes:
Pour la formule de Simpson:
Pour la formule de Newton-Cotes (
):
Remarque
Le calcul de
pour ces formules n'est pas
difficile. Considérons par exemple la formule de Newton-Cotes avec
. Nous constatons que
ne change pas de signe sur
et en utilisant la
remarque
, nous obtenons:
Exercice
Noyau de Peano
V Exemples de calcul numérique de l'ordre
Intégration numérique
→ V Exemples de calcul numérique de l'ordre
V-1 Préliminaires
Intégration numérique
→
V Exemples de calcul numérique de l'ordre
→ V-1 Préliminaires
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Ici nous allons vérifier à l'aide de Matlab l'ordre de quelques
méthodes de quadrature déjà étudiées précédemment pour
approcher la valeur de l'intégrale
avec
et une subdivision de plus en plus fine de l'intervalle
correspondante à
V-2 Méthode des rectangles à gauche
Intégration numérique
→
V Exemples de calcul numérique de l'ordre
→ V-2 Méthode des rectangles à gauche
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On note
l'approximation de
par la méthode des
rectangles à gauche et
l'erreur commise. On affiche les
valeurs de
,
,
,
, et
.
Code Matlab
Les résultats obtenus par ce programme sont:
Commentaires:
On constate que se stabilise autour de 2.5e-01 alors que explose au fur et à mesure que augmente (les subdivisions de plus en plus fines). Ceci confirme le fait que cette méthode est d'ordre 1.
clear all;
fid = 1;
fmt = '%% %10d %20.9e %20.9e %20.9e %20.9e \n';
for j = 1:2:17
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
Iexa = log(2);
alpha = 1;
beta = 2;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Irg = 0.0;
for i = 1:N
Irg = Irg + h*f(x(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
%Irg
Erg = abs(Iexa - Irg) ;
Erg1 = abs(Iexa - Irg)/h ;
Erg2 = abs(Iexa - Irg)/h^2 ;
%%%%%%%%%%%%%%%%%%%%%%%%
fprintf(fid, fmt, j, Irg, Erg, Erg1, Erg2);
end
Les résultats obtenus par ce programme sont:
j Irg Erg Erg/h Erg/h^2
1 8.333333333e-01 1.401861528e-01 2.803723055e-01 5.607446111e-01 3 7.253718504e-01 3.222466981e-02 2.577973585e-01 2.062378868e+00 5 7.010207083e-01 7.873527709e-03 2.519528867e-01 8.062492374e+00 7 6.951041202e-01 1.956939668e-03 2.504882775e-01 3.206249952e+01 9 6.936357002e-01 4.885196685e-04 2.501220703e-01 1.280625000e+02 11 6.932692658e-01 1.220852137e-04 2.500305176e-01 5.120625000e+02 13 6.931776991e-01 3.051850945e-05 2.500076294e-01 2.048062500e+03 15 6.931548100e-01 7.629452736e-06 2.500019072e-01 8.192062496e+03 17 6.931490879e-01 1.907352286e-06 2.500004788e-01 3.276806276e+04
Commentaires:
On constate que se stabilise autour de 2.5e-01 alors que explose au fur et à mesure que augmente (les subdivisions de plus en plus fines). Ceci confirme le fait que cette méthode est d'ordre 1.
V-3 Méthode des trapèzes
Intégration numérique
→
V Exemples de calcul numérique de l'ordre
→ V-3 Méthode des trapèzes
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On note l'approximation de par la méthode des trapèzes et l'erreur commise. On affiche les valeurs de , , , , , et .
Code Matlab
clear all;
fid = 1;
fmt = '%% %10d %12.9e %12.9e %12.9e %12.9e %12.9e \n';
for j = 1:2:17
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
Iexa = log(2);
alpha = 1;
beta = 2;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Itr = 0.0;
for i = 1:N
Itr = Itr + h*(0.5*f(x(i)) + 0.5*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Etr = abs(Iexa - Itr) ;
Etr1 = abs(Iexa - Itr)/h ;
Etr2 = abs(Iexa - Itr)/h^2 ;
Etr3 = abs(Iexa - Itr)/h^3 ;
%%%%%%%%%%%%%%%%%%%%%%%%
fprintf(fid, fmt, j, Itr, Etr, Etr1 , Etr2, Etr3);
end
Les résultats obtenus par ce programme sont:
j Itr Etr Etr/h Etr/h^2 Etr/h^3
1 7.08333e-01 1.51862e-02 3.03723e-02 6.07446e-02 1.21489e-01 3 6.94122e-01 9.74670e-04 7.79736e-03 6.23789e-02 4.99031e-01 5 6.93208e-01 6.10277e-05 1.95289e-03 6.24924e-02 1.99976e+00 7 6.93151e-01 3.81467e-06 4.88278e-04 6.24995e-02 7.99994e+00 9 6.93147e-01 2.38418e-07 1.22070e-04 6.25000e-02 3.20000e+01 11 6.93147e-01 1.49012e-08 3.05176e-05 6.25000e-02 1.28000e+02 13 6.93147e-01 9.31321e-10 7.62938e-06 6.24999e-02 5.11999e+02 15 6.93147e-01 5.82108e-11 1.90745e-06 6.25033e-02 2.04811e+03 17 6.93147e-01 3.63654e-12 4.76648e-07 6.24752e-02 8.18875e+03
Commentaires:
On constate que se stabilise autour de 6.25e-02 alors que explose au fur et à mesure que augmente. Ceci confirme le fait que cette méthode est d'ordre 2.
V-4 Méthode de Simpson
Intégration numérique
→
V Exemples de calcul numérique de l'ordre
→ V-4 Méthode de Simpson
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
On note l'approximation de par la méthode de Simpson et l'erreur commise. On affiche les valeurs de , , , , , et .
Code Matlab
clear all;
fid = 1;
fmt = '%% %3d %12.5e %12.5e %12.5e %12.5e %12.5e \n';
for j = 1:1:10
%%%%%%%%%%%%%%%%%%%%%%%%
% Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
Iexa = log(2);
alpha = 1;
beta = 2;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Isi = 0.0;
for i = 1:N
Isi = Isi + h*(1/6*f(x(i)) + 2/3*f((x(i) + x(i+1))/2) + 1/6*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Esi = abs(Iexa - Isi) ;
Esi3 = abs(Iexa - Isi)/h^3 ;
Esi4 = abs(Iexa - Isi)/h^4 ;
Esi5 = abs(Iexa - Isi)/h^5 ;
%%%%%%%%%%%%%%%%%%%%%%%%
fprintf(fid, fmt, j, Isi, Esi, Esi3 , Esi4, Esi5);
end
Les résultats obtenus par ce programme sont:
j Isi Esi Esi/h^3 Esi/h^4 Esi/h^5
1 6.93254e-01 1.06788e-04 8.54302e-04 1.70860e-03 3.41721e-03 2 6.93155e-01 7.35009e-06 4.70406e-04 1.88162e-03 7.52650e-03 3 6.93148e-01 4.72259e-07 2.41797e-04 1.93437e-03 1.54750e-02 4 6.93147e-01 2.97299e-08 1.21774e-04 1.94838e-03 3.11740e-02 5 6.93147e-01 1.86151e-09 6.09979e-05 1.95193e-03 6.24619e-02 6 6.93147e-01 1.16398e-10 3.05130e-05 1.95283e-03 1.24981e-01 7 6.93147e-01 7.27574e-12 1.52583e-05 1.95307e-03 2.49992e-01 8 6.93147e-01 4.54081e-13 7.61822e-06 1.95026e-03 4.99268e-01 9 6.93147e-01 2.80886e-14 3.76999e-06 1.93024e-03 9.88281e-01 10 6.93147e-01 2.66454e-15 2.86102e-06 2.92969e-03 3.00000e+00
Commentaires:
On constate que se stabilise autour de 1.95e-03 alors que explose au fur et à mesure que augmente. Ceci confirme le fait que cette méthode est d'ordre 4.
VI Bibliographie
Intégration numérique
→ VI Bibliographie
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
- Philipe G. Ciarlet. Introduction à l'analyse numérique et à l'optimisation . Dunod 1990.
- Jean-Pierre Demailly. Analyse numérique et équations différentielles . Presses Universitaires de Grenoble, 1996.
- Ernst Hairer. Introduction à l'analyse numérique . Université de Genève, section mathématiques, case postale 240. Octobre 2001.
VII Exercices
Intégration numérique
→ VII Exercices
- I Introduction
- II Formules de quadrature et leur ordre
- III Mise en oeuvre sur Matlab
- IV Etude de l'erreur d'une méthode de quadrature
- V Exemples de calcul numérique de l'ordre
- VI Bibliographie
- VII Exercices
- Index
Exercice
Soit
une fonction de classe
. On
considère la méthode d'intégration numérique approchée
donnée par
- Calculer l'ordre de cette méthode en fonction de .
- On se place dans le cas où cette méthode est d'ordre
.
- Calculer le noyau de Peano et tracer le graphe de pour . Pour quelles valeurs de le noyau est-il de signe constant?
- Montrer que l'erreur
vérifie la majoration
où est une constante dont on déterminera la valeur optimale
- lorsque est de signe constant.
- lorsque .
Exercice
On rappelle que par construction, les méthodes de Newton-Cotes sont les formules de
quadratures élémentaires de type
telles que les noeuds
soient équidistants et centrés
dans l'intervalle
, les
étant choisis de telle façon que ces formules
soient exactes pour tout polynôme
de degré inférieur ou égale à
. Montrer
que si
est pair ces formules sont aussi exactes pour les polynômes de degré
.
(Indication : on pourra remarquer que
et en tirer les conséquences
pour les polynômes impairs.)
Exercice
Construire les formules d'intégration numérique suivantes :\
\
\
Déterminer leur noyau de Peano et en déduire l'erreur commise.
\
\
Déterminer leur noyau de Peano et en déduire l'erreur commise.
Exercice
- Montrer que (Indication : appliquer la formule d'Euler-MacLaurin à entre et .)
- Montrer que si
est une fonction périodique de période
, alors
et où représente l'évaluation de la formule des trapèzes de pas pour sur
Exercice
Soient
et
deux points de
et
et
.
On considére la formule d'itégration suivante :
Quelles conditions doivent vérifier
et
pour que cette formule soit exacte pour
- les fonctions constantes?
- les fonctions affines?
- les polynômes de degré inférieur ou égale à ?
Exercice
On considère la formule d'intégration suivante :
- Déterminer les valeurs de
et
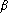 pour que
soit exacte sur
.
pour que
soit exacte sur
.
- En déduire les valeurs de
et
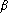 pour que
soit d'ordre le plus élevé possible.
pour que
soit d'ordre le plus élevé possible.
-
- Calculer le noyau de Peano dans le cas où est d'ordre et vérifier que ce noyau est une fonction paire.
- En déduire qu'il existe tel que où est l'erreur d'intégration.
- Donner la formule d'intégration relative à sur
- Estimer l'erreur d'intégration obtenue par la méthode composée associée à sur avec un pas constant .
Exercice
On considére la formule d'intégration suivante :
- Déterminer et de sorte que cette formule soit exacte sur .
- Calculer alors l'ordre de cette méthode.
Exercice
- Soit
. Montrer qu'il existe un
polynôme
unique de degré
vérifiant: Déterminer et la comparer à .
- On considére
. On veut calculer cette intégrale avec une erreur inférieur à
.
- Déterminer le pas nécessaire pour la méthode des trapèzes.
- Déterminer le pas nécessaire pour la méthode de Simpson.
Exercice
- Trouver l'ordre des formule de : rectangle, trapèze et Simpson.
- Pour
. On pose
Montrer que .
- En déduire . Calculer par deux méthodes différentes .
- Enoncer le thérème de Peano et montrer que si
alors on a :